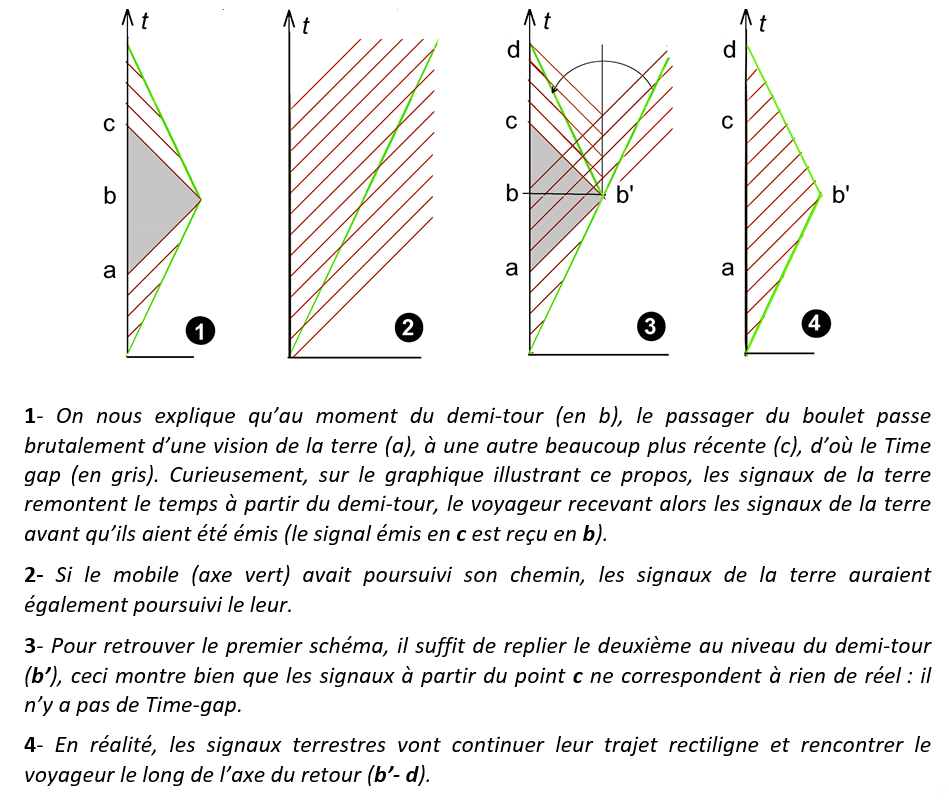
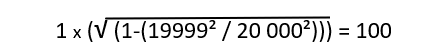La combinaison de l’effet Doppler et de ceux de la Relativité restreinte

Avant d’accepter une affirmation, il faut toujours vérifier sur quoi elle est fondée. Lorsqu’on nous dit que la théorie de la relativité interdit de constater le mouvement inertiel par des moyens physiques, quel en est le fondement ?

L’origine vient de Galilée, qui a constaté que dans la cale d’un navire en mouvement régulier, les mesures physiques sont identiques à celles effectuées alors que le navire était immobile au port. C’est un constat, rien de plus. Il va de soi que si on monte sur le pont du navire, il est aisé de voir si le vent gonfle les voiles et l’étrave fend la mer. La conclusion est que seules des mesures externes permettent de constater un mouvement inertiel. D’ailleurs, même en restant dans la cale pendant tout le trajet, le passager du navire constatera rétroactivement le mouvement, en voyant qu’il est arrivé à destination.

L’origine vient de Galilée, qui a constaté que dans la cale d’un navire en mouvement régulier, les mesures physiques sont identiques à celles effectuées alors que le navire était immobile au port. C’est un constat, rien de plus. Il va de soi que si on monte sur le pont du navire, il est aisé de voir si le vent gonfle les voiles et l’étrave fend la mer. La conclusion est que seules des mesures externes permettent de constater un mouvement inertiel. D’ailleurs, même en restant dans la cale pendant tout le trajet, le passager du navire constatera rétroactivement le mouvement, en voyant qu’il est arrivé à destination.

L’impossibilité de déceler le mouvement en interne est due à la loi d’addition des vitesses de Newton. A bord du navire (ou de tout corps en mouvement), tout ce qu’il contient est entraîné à la vitesse de celui-ci. La vitesse des mouvements propres effectués en interne s’ajoute à celle due à l’entraînement et seule la différence apparaît, si bien que rien ne permet de mettre le mouvement en évidence.

Revenons aux faits, c’est à dire à l’histoire du voyage en boulet de Paul Langevin.

• Alors que pour les terriens le périple du voyageur a duré 200 ans, il ne s’est écoulé que deux ans pour ce dernier. Le voyageur a donc vécu au ralenti.
• A l’aller, les terriens et le voyageur constatent un ralentissement temporel réciproque et dans les mêmes proportions. Pendant le retour, ils constatent une accélération temporelle réciproque et identique.

La théorie de la relativité prévoit un ralentissement du temps à bord du mobile observé. D’où vient alors cette étrange symétrie décrite par Langevin ? D’aucuns expliquent cela par la relativité du mouvement. De deux corps en mouvement relatif, il est impossible de déterminer lequel se meut, chacun pouvant se dire immobile et l’autre en mouvement, d’où la symétrie. Ainsi, lorsque le navire arrive à destination, on pourrait dire que c’est lui qui a fait le trajet… ou que le port de destination est venu à sa rencontre. Voila pourquoi les constats des terriens et du voyageur sont identiques. C’est peut-être logique, mais bizarre tout de même.

Revenons à la relativité du mouvement. S’il est impossible de déterminer lequel des deux corps en mouvement relatif se meut, c’est faute d’un repère pouvant être considéré comme immobile dans un univers en expansion. En pratique, il est toujours possible de trouver un système de référence commun et le choix de celui-ci dépend de ce qu’il s’agit de démontrer. La vitesse relative est la somme des vitesses propres des mobiles concernés, il ne peut donc y avoir de valeur relative sans vitesses propres, même si nous ne pouvons connaître que le résultat de leur cumul. Seule l’ignorance de celles-ci nous donne l’illusion de la symétrie des situations.

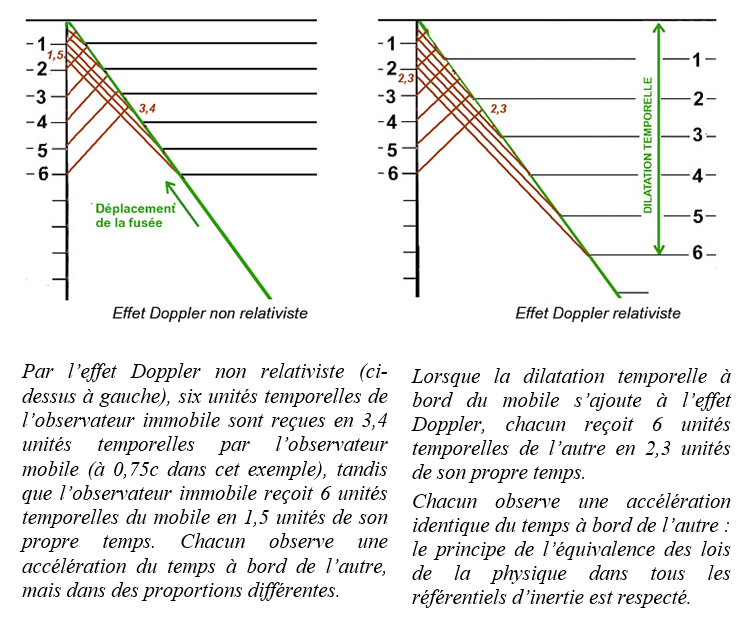
La relativité du mouvement est un bien mauvais candidat pour expliquer la symétrie décrite dans l’histoire du voyageur en boulet. Paul Langevin tient compte de l’effet Doppler dans ses calculs. Bien sûr, l’effet Doppler est dissymétrique, alors que les observations réciproques des terriens et du voyageur sont symétriques, mais il faut également tenir compte de l’inflation temporel qui affecte le seul voyageur. Pour vérifier que le cumul de l’effet Doppler et de la dilatation temporelle aboutit à la symétrie des observations, il suffit de faire le calcul.

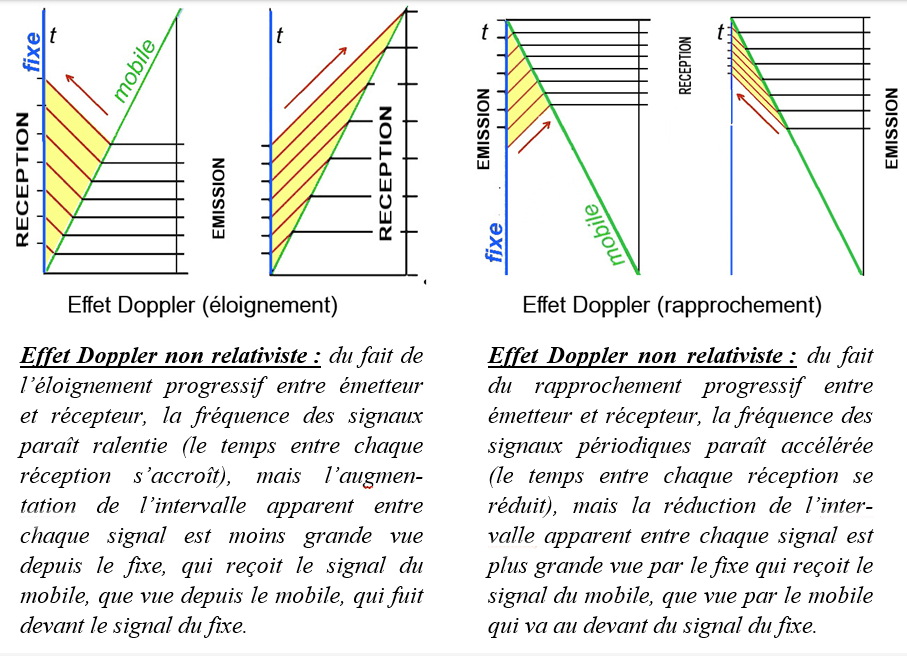
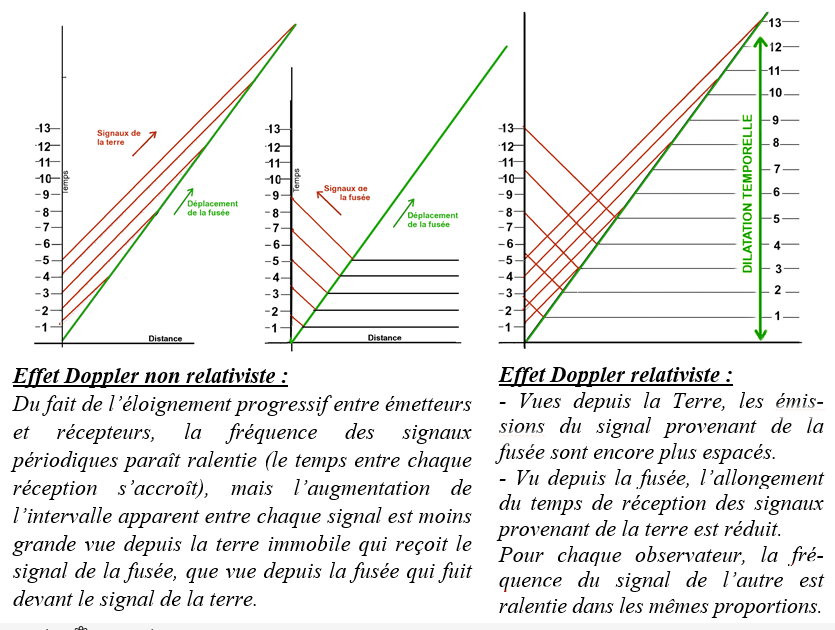
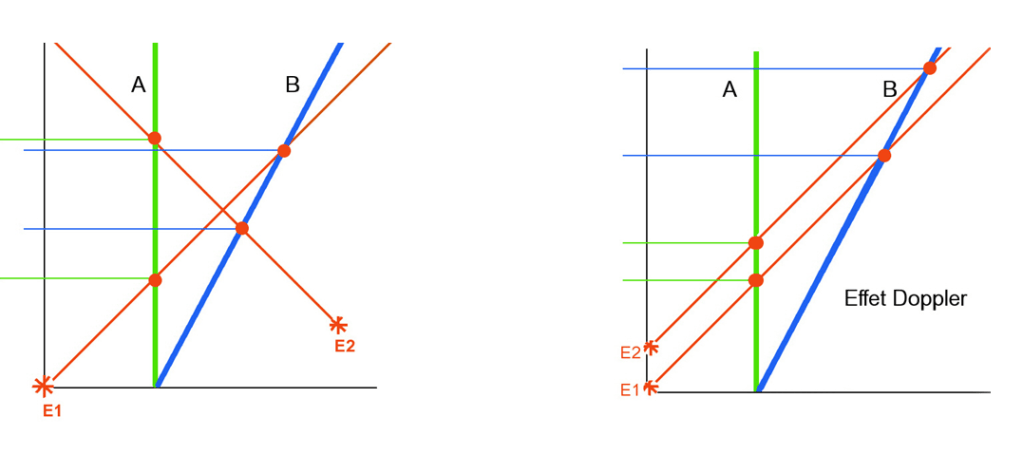
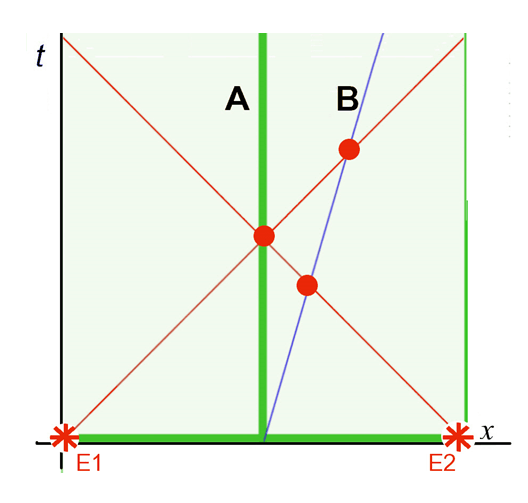
L’inflation temporelle à bord du mobile à un double effet : ses signaux sont émis à une fréquence moins élevée et son passager perçoit les signaux du fixe comme accélérés. Ces effets sont indépendants du sens du déplacement du mobile relativement au fixe. La combinaison de l’effet Doppler et de l’inflation temporelle relativiste égalise la fréquence perçue par le fixe et le mobile. Lorsqu’ils s’éloignent, les signaux du mobile, modérément ralentis par l’effet Doppler, sont encore ralentis par le ralentissement temporel de l’émetteur. Les signaux émis par le fixe, très ralentis par l’effet Doppler, sont accélérés par le ralentissement à bord du mobile qui les reçoit. Il en résulte une égalisation des observations. Lorsque le mobile se rapproche du fixe, la distance se réduit à chaque émission d’un signal, ce qui en contracte la fréquence pour le récepteur : le temps semble s’accélérer. Le mobile va au-devant des signaux du fixe, ce qui modère la contraction perçue de la fréquence par le voyageur. Cependant les signaux du mobile sont plus espacés du fait du ralentissement temporel, ce qui a pour effet de ralentir la réception vue par la terre et d’accélérer celle vue depuis le mobile. Comme pour l’éloignement, les constats sont identiques lorsque le mobile se rapproche. Il faut bien remarquer que l’égalité des observations pendant le voyage est due à la combinaison d’une illusion (l’effet Doppler) et d’un ralentissement réel (effet relativiste). Au retour du voyageur sur terre, la symétrie apparente disparaît lorsque disparaît l’illusion. Lorsqu’il partage le même référentiel que son jumeau, seul subsiste la désynchronisation des temps, qui est irréversible

Il n’y a pas de paradoxe, mais des conséquences

Tant que dure le mouvement de translation uniforme ou inertiel, l’impossibilité de le constater par des mesures internes demeure. Si le voyageur s’était éloigné éternellement, jamais l’écart des âges n’aurait pu être mis en évidence, faute pour les jumeaux de pouvoir se comparer. Cependant, la relativité du mouvement est une illusion due à l’absence d’information sur le mouvement réel lorsque celui-ci est inertiel, car il ne produit en principe aucun effet décelable. Le constat de Galilée, au fond de sa cale de navire, ne signifie pas autre chose. L’impossibilité de constater le mouvement n’interdit pas qu’il ait lieu. Le constat de la différence des âges prouve seulement la réalité du mouvement… lorsque le mouvement relatif a cessé.

Si la réalité du mouvement peut être constatée lorsque les voyageurs se retrouvent sur le même référentiel, c’est donc que la réciprocité des observations en phase inertielle est une illusion. Nous avons montré que le ralentissement du rythme temporel est lié à la vitesse et non à l’accélération, ce qui en fait une conséquence de tout mouvement, même en l’absence d’effet observable. Ainsi le mouvement est-il une réalité et la relativité du mouvement en phase inertielle une illusion. Si nous ne pouvons désigner d’observateur privilégié, c’est parce que tous sont en mouvement et que nous ne disposons pas de repère fixe. Le mouvement est évidemment relatif si on ne considère que son aspect topographique (le déplacement), mais il est absolu relativement à celui de la lumière, même si la vitesse reste une notion relative, puisqu’elle se calcule par le temps mis à parcourir la distance comprise entre deux points.

Si nous admettons cela, alors tout devient plus simple. La réalité objective est bien conforme à ce que nous suggère le bon sens, sauf qu’elle est inaccessible à l’observation, faute de repère. L’étrangeté vient de là et du caractère local du temps lié à la vitesse, il est vrai complété par la contraction des longueurs, toute aussi étrange.

L’histoire des jumeaux continue d’alimenter la chronique, sans clore le débat. Pourtant, en vérité, dans son récit du voyageur en boulet, tout était dit par Paul Langevin dès le début.

Pour Einstein (et Langevin), les effets relativistes sont réels

La façon la plus simple et la plus logique de résoudre le paradoxe des jumeaux est d’admettre la réalité physique du ralentissement temporel à bord du référentiel en mouvement inertiel. Pour Paul Langevin, la réalité des effets relativistes ne faisait d’ailleurs aucun doute et il ne pensait certainement pas que son exemple soulèverait autant de polémiques. Einstein avait d’ailleurs déjà raconté une histoire semblable dès 1911 et il a toujours affirmé la réalité du ralentissement temporel et de la contraction des longueurs :

« Si l’on plaçait un organisme vivant dans une boîte, (…) on pourrait faire en sorte qu’après un long voyage, il revienne à son point de départ à peine modifié, alors que des organismes correspondants, restés sur place, auraient depuis longtemps été remplacés par des générations ultérieures. Pour les organismes mobiles, le long voyage n’aurait duré qu’un instant pourvu que le déplacement ait été effectué à une vitesse proche de celle de la lumière.[1]» Ne reconnaît on point là notre histoire de jumeaux ? L’inventeur de la théorie de la Relativité restreinte avait donc envisagé la même expérience que Paul Langevin pour illustrer une conséquence de la grande vitesse d’un référentiel en mouvement inertiel, sans y voir le moindre paradoxe.

Pour Einstein, il ne faisait aucun doute que le ralentissement temporel est réel. Dès sa première communication[2], en 1905, il affirmait que les horloges en mouvement retardent réellement : « Si nous faisons l’hypothèse que le résultat obtenu sur une ligne droite est également vrai pour une ligne courbe, nous obtenons le théorème suivant : Si à A, il y a deux horloges synchronisées et si nous déplaçons l’une d’elles à une vitesse constante selon une courbe fermée qui revient en A, le déplacement étant réalisé en t secondes, alors à son arrivée à A, cette dernière retardera de ½t(v/c)² secondes sur l’horloge immobile ».

Il a par ailleurs précisé dans son ouvrage publié en 1916 : « Lorentz et Fitzgerald supposèrent que le mouvement du corps par rapport à l’éther produit en lui un raccourcissement dans la direction de son mouvement, qui fait précisément disparaître la différence de temps […]. Une comparaison avec les réflexions du chapitre 12 montre que ce moyen était aussi bon au point de vue de la Théorie de la relativité. [3]» Ce qui différencie Einstein de Lorentz, ce n’est pas le caractère apparent ou non des effets de la transformation de Lorentz, mais qu’Einstein n’a pas besoin de l’éther pour sa théorie. Ce n’est pas le vent d’éther qui contracte le mobile, mais sa vitesse.

Finalement, le plus curieux est que des commentateurs, par ailleurs fort compétents, acceptent la théorie de la Relativité restreinte sans entendre les arguments de son auteur. Einstein disait fort justement : « Depuis que les mathématiciens se sont emparés de la théorie de la Relativité, je n’y comprends plus rien moi-même »[4].

Si le mouvement ralentit l’écoulement du temps, il est normal que le voyageur revienne plus jeune que le terrien resté à l’attendre. La question de savoir si les effets relativistes sont une réalité ou un simple effet d’observation est donc tranchée dès lors que diverses expériences ont montré la réalité de la désynchronisation des horloges. L’histoire des jumeaux n’est pas un paradoxe, mais la preuve de la réalité du ralentissement temporel prévu par la théorie de la Relativité restreinte. Pourquoi, en ce cas, certains y voient-ils toujours un paradoxe contredisant la théorie de la Relativité ? Tout simplement parce qu’ils pensent que la symétrie en mouvement relatif est réelle : si le boulet s’éloigne de la terre, il est aussi vrai que la terre s’éloigne de la fusée. Si le voyageur à vieilli d’une certaine durée, le terrien doit donc avoir vieilli de même. Comme ils doivent bien admettre la réalité du ralentissement des horloges démontrée par l’expérimentation, les partisans du paradoxe l’attribuent aux phases non inertielles du voyage. L’explication du ralentissement constaté est ainsi recherchée en dehors de le Relativité restreinte. 

Nous avons déjà dit ce qu’il convient de penser de la symétrie du mouvement relatif, mais ceux qui croient à sa réalité sont confortés dans leur opinion par la réciprocité des observations entre l’observateur immobile et celui en mouvement. Lorsque l’observateur immobile voit le temps ralentir à bord du mobile, le passager de ce dernier constate le même ralentissement chez le premier.

[1]  Albert EINSTEIN, « Die Relativitätstheorie », Naturforschende Gesellschaft, n°56, 1911, pages 1 à 14.

[2] Albert EINSTEIN: « Zur Elektrodynamik bewegter Körper », in Annalen der Physik, vol. 322, no 10, 26
   septembre 1905, p. 891-921. 

[3] Albert EINSTEIN, La Théorie de la relativité restreinte et générale, chapitre 16, 1916, édition française
   Gauthier-Villars 1956).

[4] CLARK Ronald William : « Einstein, sa vie et son époque, Paris, Stock, 1980 ».

Remarque sur le ralentissement du temps

Lorsque l’on dit qu’à bord d’un référentiel plus rapide le temps est ralenti, d’aucuns se récrient en disant qu’il n’en est rien ou que cette affirmation n’a aucun sens, que ce sont des balivernes, mais généralement sans autre explication ou bien en prétendant que les référentiels parcourent un trajet différent dans l’espace-temps[1], ce qui n’est qu’une pirouette. Certes, l’écoulement du temps est perçu de la même façon dans tous les référentiels, quelle que soit leur vitesse, c’est leur temps propre. Pour cette raison, il est inutile d’espérer vivre plus longtemps en se déplaçant très vite. C’est par comparaison entre eux que la différence d’écoulement du temps apparaît aux observateurs et encore cet effet est-il perçu comme réciproque ! En comparant son temps propre avec celui qu’il mesure à bord du référentiel observé, ou temps impropre, ce dernier sera toujours plus lent s’il s’éloigne et plus rapide s’il se rapproche. De là à conclure que les effets sont symétriques, en véritable effet miroir, il n’y qu’un pas… qu’il faut se garder de franchir. En vérité, le ralentissement temporel est physiquement réel à bord du référentiel en mouvement et la réciproque n’est qu’une illusion due aux effets de la relativité ; nous y reviendrons. Lorsque l’illusion se dissipe, l’observateur le plus lent trouve que le plus rapide a vieilli moins vite que lui et le plus rapide trouve que le plus lent a vieilli en accéléré, mais chacun a le sentiment d’avoir vécu normalement le temps marqué par son horloge : son temps propre. La raison en est que ce n’est pas seulement un problème d’horloge, mais un ralentissement de tous les mouvements du référentiel en mouvement, y compris celui du vieillissement des cellules et du fonctionnement des neurones de l’observateur. N’en déplaise à ceux qui trouvent la formulation inappropriée, nous parlerons donc de ralentissement temporel dans les pages qui suivent.

On nous dit, parfois, qu’il est théoriquement possible de voyager dans le futur, à condition de se mouvoir à grande vitesse. Cela est faux, car nous voyageons tous vers le futur quelle que soit notre vitesse, il suffit pour cela de vieillir, de laisser passer le temps. La seule différence est que le temps passe moins vite pour celui qui se meut. Cependant, il ne s’agit pas d’un véritable voyage, avec billet d’aller-retour. Il s’agit plutôt d’un exil dans le futur, sans espoir de retour.

[1] Sean CARROL : L’univers à notre portée – Espace, temps et mouvement, p. 186,   Quanto, 2023.

Il n’est pas nécessaire de comprendre ma théorie pour
en faire l’application. Max Planck : Initiations
à la physique

,
Alors que Paul Langevin ne songeait qu’à illustrer la théorie de la Relativité restreinte, son histoire de voyageur en boulet est à l’origine du fameux « paradoxe des jumeaux ». Le récit initial a été quelque peu enjolivé : le boulet remplacé par un vaisseau spatial et le voyageur doté d’un jumeau resté à terre. Au retour du vaisseau, les jumeaux constatent que le voyageur est resté plus jeune : le fond de l’affaire reste donc le même.

Certains, cependant, se sont avisés que la différence des âges contredit un principe dont ils pensent qu’il est un fondement du principe de relativité : la symétrie entre référentiels inertiels. Le paradoxe n’est pas que les jumeaux vieillissent à un rythme différent, mais que cela se produise pendant le mouvement inertiel. Ils en ont conclu que le ralentissement temporel et la contraction des longueurs, prévus par la théorie de la Relativité, n’étaient que des effets d’observation et non des effets affectant réellement les corps en mouvement.

Le refus de la réalité des effets relativistes

Voici ce qu’en dit Louis de Broglie, lauréat du prix Nobel de physique en 1929 : « Il y a […] une différence essentielle entre la contraction de Lorentz-Fitzgerald et celle qui résulte, d’après Einstein, de la transformation de Lorentz. La première, en effet, était censée être une contraction réelle provoquée par le mouvement absolu du corps dans l’éther, tandis que la seconde est la contraction apparente relative au second observateur [….]. La contraction apparente des longueurs a comme complément le ralentissement apparent des horloges. […] qui résultent des nouvelles définitions de l’espace et du temps auxquelles est liée la transformation de Lorentz. […] Les raisonnements par lesquels M. Einstein a justifié sa nouvelle conception de l’espace et du temps sont souvent subtils et délicats à développer correctement, mais ils sont parfaitement solides et du point de vue logique, aucune critique sérieuse n’a pu leur être adressée[1]. En particulier, on peut parfaitement justifier le fait paradoxal que la contraction des règles et le ralentissement des horloges sont des apparences réciproques, c’est-à-dire que si deux observateurs en mouvement relatif uniforme sont munis chacun d’une règle et d’une horloge, les deux règles et les deux horloges étant de constitution identique, chacun des observateurs trouve que la règle de l’autre est plus courte que la sienne et que l’horloge de l’autre retarde sur le sienne. Si surprenante que puisse paraître au premier abord cette réciprocité, elle s’explique aisément quand on en examine avec soin la théorie, ce que naturellement nous ne pouvons faire ici ».

Einstein aurait-il été partisan du caractère seulement apparent de la contraction des longueurs et de la dilatation du temps ? Il dit explicitement le contraire : « Il est à priori évident que nous devons tirer des équations de transformation quelques renseignements sur le comportement physique des règles et des horloges ». Quelques lignes plus loin, il ajoute :  Par suite de son mouvement, l’horloge marche plus lentement que lorsqu’elle est au repos. » [2]. Les auteurs qui refusent le caractère réel des effets relativistes avancent principalement deux explications du moindre vieillissement du jumeau voyageur : les phases non inertielles du trajet (accélérations et décélérations) et le changement de référentiel au moment du demi-tour.

[1] La physique nouvelle et les quanta, Flammarion 1937, chapitre IV Ces commentaires montrent que Louis de Broglie ne comprenait pas vraiment la théorie développée par Einstein.

[2] Albert Einstein, La Théorie de la relativité restreinte et générale, chapitre 12, 1916, édition française Gauthier-Villars 1956).

L’explication par les accélérations et décélérations subies (phases non inertielles)

Parce qu’ils refusent la réalité des effets relativistes, de nombreux commentateurs ont prétendu résoudre le soi-disant paradoxe en sortant de la Relativité restreinte que Paul Langevin voulait précisément illustrer. Puisque la différence d’âge ne peut être le fait du mouvement inertiel, c’est donc pendant les phases non inertielles du voyage que le ralentissement temporel a eu lieu : accélération du départ, demi-tour puis freinage à l’arrivée. La symétrie des référentiels en mouvement inertiels est sauvée et comme cet argument est présenté à l’occasion d’un exposé sur la Relativité restreinte (ne traitant que des mouvements inertiels), les auteurs ne se croient pas obligés d’expliquer comment les changements d’allure produisent un tel effet. Le raisonnement est de pure logique formelle, il repose uniquement sur l’impossibilité supposée du ralentissement temporel en phase de mouvement inertiel. Quelques auteurs renvoient à la Relativité générale, qui traite de la gravitation, mais sans autre explication.

Il est plaisant cependant de constater que le moindre vieillissement du voyageur, constaté à son retour, est expliqué par des phases du voyage que Langevin avait écarté pour ne pas compliquer les calculs. En toute logique, les phases non inertielles sont déterminées par la vitesse de croisière devant être atteinte et non par la durée où celle-ci est maintenue. Si l’accélération était la cause du moindre vieillissement du voyageur, cet effet ne devrait pas être fonction de la durée du voyage, or pour obtenir la durée vécue par l’astronaute il faut diviser par γ la durée mesurée par le terrien. On voit bien que l’accélération n’est pour rien là-dedans ! La confusion vient en partie de Paul Langevin lorsqu’il fait observer que seul le voyageur ressent l’accélération au milieu du voyage, mais c’était pour souligner qu’il est le seul à constater être en mouvement et que cela rompt la symétrie des observations, le terrien ne ressentant rien de tel à l’occasion du demi-tour.

Pour apprécier l’incohérence de l’explication proposée, revenons aux calculs de Langevin.
Le voyage a duré 200 ans pour les terriens et seulement 2 ans pour le voyageur. Si le temps du voyageur s’est écoulé comme sur terre pendant la phase inertielle, la durée de celle-ci ne peut être supérieure au temps vécu par lui, c’est à dire 2 ans, ce qui suppose que le temps a été complètement suspendu pendant les accélérations et décélérations ayant durées 198 ans. Si tel était le cas, nous le saurions, il faut donc en conclure que le ralentissement temporel est progressif, ce qui ampute d’autant le temps de trajet inertiel. Les périodes d’accélération et de décélération ont donc duré entre 198 ans et 200 ans… et Langevin n’en parle pas ! C’est ridicule. Sauf à conclure que les calculs sont faux, ce que personne ne prétend, cette explication ne tient pas une seconde.

L’explication par le changement de référentiel au moment du demi-tour

L’explication concurrente consiste à dire que le demi-tour provoque une rupture de symétrie. Le voyageur saute d’un référentiel qui s’éloigne, dans un référentiel qui s’approche. La Relativité restreinte ne s’appliquerait donc pas. Reste à expliquer comment le changement de référentiel a bien pu suspendre le temps du voyageur, pendant ce qu’on appelle le « time-gap ». Pour certains, la terre aurait brusquement vieilli pendant le demi-tour. Conscients du ridicule d’une telle proposition, d’autres disent que c’est le voyageur qui a enjambé le temps qui manque, mais sans dire comment. Les partisans de cette explication peuvent se réclamer d’Einstein. Selon les propos rapportés par Charles Normann[1], d’un échange entre le physicien et Paul Painlevé en 1922, à l’objection soulevée par Painlevé de la contradiction entre le ralentissement de l’horloge mobile et la réciprocité des observations découlant de la relativité en mouvement inertiel, Einstein aurait répondu que, même en considérant seulement les phases où la vitesse du plus rapide est constante, le mobile à l’aller et le mobile au retour ne constituent pas un même système de référence, mais deux systèmes de référence différents.

Le changement de référentiel n’a pas pour effet d’avaler le temps du voyageur, mais simplement de changer les conditions d’observation. Il y a bien, en effet, rupture de symétrie, en ce sens que la réciprocité des observations suppose un mouvement relatif continu. La symétrie n’est qu’apparente et ne dure qu’autant que dure le mouvement continu. Il y a bien deux référentiels distincts en cas d’aller-retour, car, à cause de l’effet Doppler, chacun observe un ralentissement du temps chez l’autre à l’aller et une accélération au retour. Par ailleurs, en tenant compte, non pas d’observations ponctuelles, mais de la durée totale du voyage, il apparaît que le trajet du boulet de Langevin est réparti en deux parties de durée égale pour le voyageur, ce qui est normal pour un aller-retour, mais que vu depuis la terre, l’aller dure deux siècles et le retour seulement deux jours. Ces anomalies permettent de distinguer qui se déplace réellement, ce qui n’aurait pas été le cas si le mobile avait continué à s’éloigner indéfiniment. Ceci démontre bien que la symétrie constatée entre deux référentiels inertiels n’est qu’un effet d’observation, une illusion fugace.

[1] « Einstein expose et discute sa théorie », Revue des deux mondes, t.9, 1922, p. 129-66.

Pour Langevin il n’y a aucun paradoxe. Pour lui, son exemple (qui ne met pas en scène des jumeaux) est parfaitement conforme à la théorie de la Relativité restreinte.

La vitesse choisie pour le boulet est inférieure d’un vingt millièmes à la vitesse de la lumière de façon constante, si bien qu’en appliquant la transformation de Lorentz, 1’année passée dans le boulet équivaut à 100 années sur terre :

Le boulet s’éloignant pendant 1 an (temps propre), puis revenant à son point de départ, le voyage total sera évalué de 2 ans dans la fusée et de 200 ans sur terre.

Un observateur terrestre assistera au demi-tour du boulet (instantané pour ne pas compliquer les choses) au bout de 199,99 ans, la vitesse de la lumière étant 1,00005 fois plus rapide que celle de la fusée :

Vitesse lumière / vitesse boulet = 1,00005

le signal d’arrivée est émis 100 ans après le départ de la terre

il met : 100 ans / 1,00005 = 99,99 ans pour arriver à la terre,

Il sera donc reçu par la terre : 100+99,99=199,99 ans après le départ du boulet.

Le boulet sera de retour sur terre au bout de deux ans selon le temps mesuré à son bord (temps propre) et de 200 ans selon les mesures terriennes (temps impropre). Sachant que le signal de demi-tour est parvenu à la terre 199,99 ans après le départ du boulet (soit 72998 jours sans tenir compte des années bissextiles) et le retour effectif sur terre 200 ans après (soit 73000 jours), le voyage de retour sera évalué à la différence par l’observateur terrestre, soit :

73000 – 72998 = 2 jours

et le voyageur a vieilli de 2 ans quand la terre a vieilli de 2 siècles.

« Pendant qu’ils s’éloigneront l’un de l’autre avec une vitesse voisine de celle de la lumière, chacun d’eux semblera à l’autre fuir devant les signaux électromagnétiques ou lumineux qui lui sont envoyés, de sorte qu’il mettra un temps très long pour recevoir les signaux émis pendant un temps donné. Le calcul montre ainsi que chacun d’eux verra vivre l’autre deux cents fois plus lentement qu’à l’ordinaire. Pendant l’année que durera pour lui ce mouvement d’éloignement, l’explorateur ne recevra de la Terre que des nouvelles des deux premiers jours après son départ ; pendant cette année il aura vu la Terre accomplir les gestes de deux jours. »

Pour calculer la différence de temps de trajet propre à chaque référentiel, Langevin utilise la transformation de Lorentz. Ensuite, ses calculs prennent en compte les vitesses d’éloignement et de rapprochement entre la terre et le boulet et de leur effet sur la transmission de l’information (effet Doppler) :

Si v/c = 0,99995, alors 1 seconde est perçue comme durant 1 + 0,99995 = 1.99995 seconde par l’effet de l’éloignement.

Au final, le facteur de dilatation temporelle étant de 100, une seconde sera perçue 1.99995 x 100 = 199,995, donc s’écoulant près de 200 fois plus lentement. Chacun verra l’autre vivre 200 fois plus lentement.

« Pour comprendre la dissymétrie, il faut remarquer que la Terre mettra deux siècles à recevoir les signaux envoyés par l’explorateur pendant son mouvement d’éloignement qui pour lui dure un an : elle le verra vivre pendant ce temps dans son arche d’une vie deux cents fois plus ralentie ; elle lui verra accomplir les gestes d’un an. A la fin de ces deux siècles parviendra à la Terre la nouvelle de la rencontre du boulet avec l’étoile qui marque le commencement du voyage du retour. L’arrivée du voyageur se produira deux jours après pendant lesquels la Terre le verra vivre deux cents fois plus vite qu’à l’ordinaire ; lui verra accomplir les gestes d’une autre année pour le trouver au retour vieilli seulement de deux ans.

Ainsi la dissymétrie tenant à ce que le voyageur seul a subi, au milieu de son voyage, une accélération qui change le sens de sa vitesse et le ramène au point de départ sur la Terre, se traduit par ce fait que le voyageur voit la Terre s’éloigner et se rapprocher de lui pendant des temps égaux chacun pour lui à un an, tandis que la Terre, prévenue de cette accélération seulement par l’arrivée d’ondes lumineuses, voit le voyageur s’éloigner d’elle pendant deux siècles et revenir pendant deux jours, pendant un temps quarante mille fois plus court. »

Vitesse du boulet : v / c = 0,99995 de la vitesse de la lumière

Vu depuis la terre :

Voyage aller du boulet : 100 ans ou 36 500 jours (sans tenir compte des années bissextiles)

Distance parcourue jusqu’au point de demi-tour : 0,9995 x 100 = 99,995 années lumières

Durée de voyage du signal d’arrivée à la vitesse de la lumière : 99,995 ans ou 36498 jours

Réception du signal d’arrivée depuis le départ du boulet : 199,995 ans ou 72998,18 jours

Durée aller retour : 200 ans ou 73000 jours

Durée apparente retour : 200 – 99,995 = 0,01 ans ou 73000 – 72998,18 = 1,83 jours

Pour le terrien, le boulet semble donc s’être éloigné pendant 99,995 ans et être revenu en 1,83 jour (chiffres arrondis à 200 ans et 2 jours par Paul Langevin), tandis que pour le voyageur, la terre s’est éloignée pendant un an et, après le demi-tour du boulet, s’est rapprochée pendant une autre année. La situation des deux jumeaux n’est donc pas symétrique du fait du retour du référentiel fusée. Sans même parler de l’écart des âges, la dissymétrie des durées de l’aller et du retour vue par chacun des jumeaux suffirait à savoir lequel était en mouvement. Quelles sont les limites de la symétrie exigée dans les référentiels d’inertie ?

La preuve par l’expérience

Les rayons cosmiques, essentiellement formés de protons, interagissent avec les atomes des couches supérieures de l’atmosphère lorsqu’ils y pénètrent, produisant de nombreuses particules, notamment des pions, qui se désintègrent à leur tour rapidement, en produisant chacun un muon et deux neutrinos. Les muons se désintègrent à leur tour avec une durée de vie moyenne de 2,2 µs (microsecondes). Ayant une vitesse presque aussi élevée que celle de la lumière, soit 300 000 km/s (300 m/µs) ils devraient parcourir, en moyenne, une distance un peu supérieure à 600 m après leur création. Les muons sont en général créés à une altitude moyenne de 30 km, or beaucoup d’entre eux parviennent jusqu’au niveau de la mer. La durée de vie moyenne du muon (t) est donc bien supérieure à celle mesurée au repos, mais conforme à la dilatation temporelle prévue par la théorie de la Relativité restreinte. Ce fait a été vérifié expérimentalement dans un accélérateur de particules, avec des résultats également conformes. Si l’on en croit les partisans de l’illusion relativiste, l’allongement de la durée de vie du muon serait seulement apparent, dû à un effet de perspective ! Pour d’autres, ce serait dû au fait que dans son référentiel les distances sont plus courtes !

Il n’est pas habituel de considérer l’effet Doppler comme un cas particulier de la relativité de la simultanéité. En réalité, ainsi nommée par Einstein dans son article fondateur de 1905, cette dernière devrait plutôt être désignée sous le nom de relativité de la réception de signaux lumineux distants, ou encore relativité de la chronologie des évènements distants. Einstein explique le mécanisme en soulignant que le mobile court vers le rayon de lumière émis devant lui et fuit celui qui vient de l’arrière. Bien évidemment, ceci n’est pas l’exclusivité des signaux émis simultanément, mais vaut pour tous les rayons lumineux rencontrés par un mobile. C’est exactement le même mécanisme qui est en œuvre dans l’effet Doppler, lequel est dû à la loi de composition des vitesses.

L’effet Doppler simple

L’effet Doppler peut se constater lorsqu’un véhicule s’approche à grande vitesse, nous dépasse puis s’éloigne. Le son est plus aigu lorsqu’il vient vers nous et plus grave lorsqu’il s’éloigne. Cela est dû au fait que la hauteur du son varie en fonction de sa fréquence d’émission ou de réception. Plus la fréquence est rapide et plus le son est aigu. Lorsque le véhicule s’approche, la fréquence de réception est accélérée, car la distance séparant l’émetteur du récepteur est de plus en plus brève, alors que lorsque le véhicule s’éloigne, la fréquence est ralentie, car la distance séparant l’émetteur du récepteur s’accroît de plus en plus.

L’effet Doppler (simple) se caractérise par la dissymétrie de son ampleur selon que l’on se place du point de vue d’un mobile percevant le signal d’un émetteur immobile, ou de celui d’un récepteur immobile recevant le signal d’un émetteur mobile.

L’effet Doppler lumineux ou relativiste

En application de la théorie de la Relativité, le temps est dilaté à bord du référentiel qui se meut (facteur de Lorentz). L’effet Doppler lumineux est la combinaison de l’effet précédemment exposé et du ralentissement temporel affectant le référentiel en mouvement L’expression « effet Doppler lumineux ou relativiste » est assez malheureuse, car elle entretient la confusion entre deux phénomènes fondamentalement différents : l’effet Doppler proprement dit qui est une illusion et le ralentissement temporel qui est réel.

Dans l’exemple ci-dessous, une fusée s’éloigne de la terre et revient vers elle à 0,75 fois celle de la lumière. La terre et la fusée émettent un signal lumineux périodique de même fréquence. A l’aller, la fréquence du signal reçu est ralentie, car du fait de l’éloignement progressif, le signal doit parcourir plus d’espace à chaque émission (effet Doppler). La fréquence du signal de la fusée vers la terre est ralenti à 1,75 pour 1, alors que la fréquence du signal terrestre vers la fusée est ralenti à 4 pour 1, car la fusée fuit devant le signal.

Cependant, l’écoulement du temps à bord de la fusée étant ralenti par l’effet relativiste, les signaux y sont émis plus lentement de la valeur du facteur γ =1,5118 et la réception de ceux venant de la terre semblent accélérés du même facteur γ. Il en résulte que les ralentissements dus à l’effet Doppler doivent être corrigés comme suit :
Signaux de la fusée : 1,75 x 1,5118 = 2,6457

Signaux de la terre : 4 / 1,5118 = 2,6457

Au retour l’effet Doppler provoque une accélération de la réception du signal, qui doit être corrigée par les effets du ralentissement temporel à bord de la fusée et conduit à uniformiser les résultats comme suit :

Signaux de la fusée : 4 / 1,5118579 = 2,6457

Signaux de la terre : 1,75 x 1,5118579 = 2,6457

L’équivalence des mesures physiques dans les référentiels en déplacement inertiel est ainsi respectée. Le ralentissement temporel à bord de la fusée à pour effet de compenser les écarts de l’effet Doppler entre la terre et la fusée. Pendant le trajet, les effets mesurés sont réciproques, mais seul le temps du voyageur s’est déroulé plus lentement et cela apparaît lorsqu’il est revenu sur terre après disparition de l’effet Doppler, car si ses horloges et ses règles se conforment à nouveau à celle du référentiel Terre, la flèche du temps ne s’inverse pas.

L’effet Doppler non relativiste est observable lorsqu’il s’agit du son, en raison de la faible vitesse de propagation des ondes sonores. Pour la lumière, seul l’effet Doppler relativiste s’applique en raison de la grande vitesse de propagation de la lumière, on parle alors d’effet relativiste lumineux. A faible vitesse, aucun ralentissement ni accélération ne sont décelables.

La cause physique du ralentissement des horloges et de la contraction des règles

Quelle est la cause du ralentissement des horloges et de la contraction des règles ? Einstein est silencieux à ce sujet. Il pose cependant la question : « Comment ? » dans l’ouvrage co-écrit avec Léopold Infield, et curieusement, il répond que « Il suit de la transformation de Lorentz, qu’un bâton se réduirait à rien… » Ainsi, la cause des effets relativistes serait une formule mathématique. Il semble bien qu’Einstein n’a pas d’explication physique du phénomène.

La théorie de la Relativité a permis de résoudre un certain nombre de problèmes et ses prédictions se sont révélées fiables. Cette théorie est donc exacte, et comme elle est fondée sur la transformation de Lorentz qui conduit à la dilatation du temps et à la contraction des règles, il faut admettre ces effets, même s’ils sont contre-intuitifs. C’est cependant un peu court comme explication. Cela revient à dire que le monde est mathématique et qu’il faut admettre toutes les conséquences d’une équation, même si on n’y comprend rien.

N’étant pas physicien, ma proposition va peut-être paraître ridicule, mais tant pis, je me lance. Partant du fait que la vitesse de la lumière ne peut être dépassée, nous devons admettre que si un atome était projeté à une vitesse proche de la lumière, la rotation ou la vibration des électrons autour du noyau serait ralentie, jusqu’à cesser totalement si la vitesse de la lumière pouvait être atteinte. A bord d’un vaisseau propulsé à une vitesse proche de celle de la lumière, tous les mouvements seraient ralentis à bord, ceux des électrons comme ceux des passagers.

Les mouvements des électrons autour du noyau seraient parfaitement circulaires en cas d’absence de toute vitesse impulsée. L’addition de la vitesse propre des électrons et de la vitesse impulsée n’a d’effet que dans le sens du mouvement, latéralement, les vitesses ne se cumulent pas totalement. De ce fait, la course des électrons étant ralentie dans le sens du mouvement impulsé, leur orbite est aplatie et devient elliptique. Il en résulte une contraction des corps dans le sens de leur déplacement.

L’explication donnée par Einstein est que lorsqu’une impulsion est donnée à un corps pour accroître sa vitesse, cela à pour effet d’augmenter sa masse par transfert d’énergie. Plus la masse d’un corps est grande et plus il faut d’énergie pour augmenter sa vitesse, donc plus il va vite et plus l’énergie nécessaire pour encore accroître sa vitesse doit être importante. Lorsqu’un corps atteint la vitesse de la lumière, il faudrait une énergie infinie pour l’accélérer encore. En outre, un corps matériel qui atteindrait cette vitesse aurait une masse infinie.

A bord d’un corps approchant la vitesse de la lumière, la vitesse propre de son contenu est ralentie jusqu’à cesser totalement lorsque la vitesse de la lumière est atteinte, car la vitesse propre du contenu ne peut plus s’ajouter à celle du corps qui le contient. En pratique, cet arrêt ne peut être brutal, il est progressif à mesure que la vitesse du contenant s’approche de celle de la lumière.

Le phénomène de contraction des longueurs est assez proche de ce qui se passe dans les trous noirs, où la force de la gravitation contracte les atomes au point que la masse d’un tel corps céleste devient gigantesque relativement à son volume. De même, tout corps en mouvement a reçu de l’énergie pour atteindre sa vitesse, ce qui accroît sa masse et contracte sa longueur dans le sens du mouvement.

Contraction des règles et contraction des distances

Il est souvent affirmé que la contraction des distances observées par le passager du référentiel en mouvement est la conséquence de la contraction des longueurs à son bord. La contraction des longueurs est invisible pour le passager, seul l’observateur externe peut la constater. Ceci est normal, car à bord du référentiel en mouvement les longueurs sont mesurées avec des règles également contractées. Il est curieux cependant que ce passager ne puisse constater la contraction de ce qu’il mesure à son bord et constate une contraction des distances dans l’espace qui l’entoure. A l’inverse, celui qui l’observe et se dit immobile, constate la contraction des longueurs du référentiel en mouvement, sans que l’espace en soit affecté de son point de vue. La contraction des distances est un phénomène qui ne peut affecter que l’espace visible par le passager du corps en mouvement.

Le simple bon sens nous dit que l’espace de l’univers est le même pour tout le monde et que si on le mesure avec une règle contractée, le résultat doit être une plus grande distance mesurée et non une plus courte. En pratique, si les longueurs se mesurent avec une règle, les distances se mesurent avec une horloge. Cependant, si l’horloge et la règle sont semblablement affectées par les effets relativistes, comment expliquer que les mesures spatiales effectues avec une règle donnent les mêmes résultats dans les deux référentiels en mouvement relatif et pas celles effectuées avec les horloges ? La raison en est qu’avec la règle on mesure des longueurs contractées comme elle, alors qu’avec l’horloge on mesure le temps mis par la lumière à parcourir une distance et que la vitesse de la lumière est invariante, non affectée par les effets relativistes dû à la vitesse. Si le rythme de l’horloge ralentit, les distances mesurées sont plus courtes. Il s’agit donc d’un effet purement observationnel. D’ailleurs, comment pourrait-on expliquer que la vitesse aurait pour effet de contracter l’espace autour du corps qui se meut sans affecter également celui de l’observateur qui se pense immobile ?

La contraction des longueurs et la contraction des distances sont donc deux phénomènes distincts, même s’il n’y a pas d’inconvénient pratique à les confondre dans les calculs, le facteur γ étant le même pour les longueurs et pour le temps. Le seul problème est que si la contraction des longueurs à bord est réelle, on en conclut que celle de l’espace l’est également, ce qui conduit à admettre autant d’espaces que d’observateurs, ce qui n’est pas une solution très économique.

Si nous admettons que les effets relativistes ne sont pas une illusion, le ralentissement des horloges et la contraction des longueurs sont réels. Pour mesurer une distance extérieure à son référentiel, tout observateur utilise un signal lumineux. S’il émet lui-même le signal, il mesure le temps de trajet aller-retour et divise par deux. Le résultat de sa mesure est directement fonction du rythme de fonctionnement de son horloge. Deux observateurs se mouvant à des vitesses différentes seront donc en désaccord sur la mesure des distances, leurs horloges respectives battant à des cadences différentes. L’écart de mesure des distances est la conséquence directe de l’écart d’écoulement temporel et dans les mêmes proportions (facteur de Lorentz).

En pratique, il suffit d’appliquer le facteur de Lorentz à la distance mesurée pour obtenir celle calculée par un observateur en mouvement dont je connais la vitesse relative. Le résultat est exact, mais ce mode de calcul peut laisser penser que c’est l’espace qui est directement contracté dans l’univers du référentiel mobile, ce d’autant plus que cela correspond très exactement à la contraction réelle des longueurs à bord du référentiel mobile. En réalité, la contraction des longueurs n’a rien à voir dans cette affaire, seul le ralentissement temporel est en cause. Il suffit que les horloges soient plus lentes pour que les distances paraissent plus courtes, sans contraction physique réelle de l’espace.

Espace et temps sont distincts, mais pour les observateurs, ils sont intimement liés car tout écart temporel conduit à un écart de mesure des distances dans les mêmes proportions. Les théories et méthodes scientifiques devant être conformes à l’observation, il est normal que cette union observée du temps et de l’espace soit prise en compte par le physicien dans ses calculs. L’espace-temps est donc une vérité scientifique puisque c’est une réalité observationnelle, mais cela n’en fait pas pour autant la réalité physique : la contraction mesurée des distances est seulement la conséquence du ralentissement temporel.

Avec un certain enthousiasme, Minkowski a écrit que « l’espace, considéré séparément, et le temps considéré séparément, sont destinés à disparaître comme des ombres », concluant que « seule une sorte d’union des deux gardera une réalité indépendante ». De quelle réalité
s’agit-il ? Minkowski n’aurait-il pas pris ses diagrammes pour la réalité ? Ce ne sont pas l’espace et le temps qui sont liés, mais leur mesure. L’espace-temps de Minkowski est le résultat de cette union, due aux particularités de la lumière par laquelle nous parvient l’information. Ce n’est pas une description de la réalité, mais de ce que nous observons. Si nous admettons cela, la théorie de la Relativité relève du sens commun, à la seule condition d’admettre l’invariance de la vitesse de la lumière et l’impossibilité de la dépasser. La mesure des distances étant faite à l’aide d’une horloge qui bat au rythme de chacun en fonction de sa vitesse, il en résulte que chacun voit le monde à sa manière, ce qui explique pourquoi il y a autant d’espace-temps que d’observateurs se mouvant à des vitesses différentes. Dans le réel, il y à l’espace commun et des observateurs qui le mesurent avec des horloges battant à des rythmes différents et obtiennent des résultats discordants. L’observateur immobile peut appliquer le facteur de Lorentz directement à ses propres mesures de distances pour passer dans l’espace-temps du mobile observé, mais c’est une facilité qui fait oublier qu’en réalité c’est le temps seul qui est concerné. Le résultat est exact, mais si l’on pense que l’espace est contracté comme l’est la longueur du mobile, l’explication est fausse et tout devient incompréhensible. Il n’y a en effet rien à comprendre lorsque nous acceptons un résultat conforme à l’observation comme étant l’expression de la réalité, sans chercher à comprendre comment il est obtenu.

Incidences sur la notion de mouvement propre et de mouvement absolu

L’impossibilité de dépasser la vitesse de la lumière a une conséquence sur la notion de mouvement absolu. Nous avons vu que rien ne s’oppose à ce que notre univers ne soit qu’un parmi d’autres, entraînés dans un même mouvement. Il est ainsi possible d’envisager une régression à l’infini en imaginant que notre groupement d’univers n’est qu’un parmi d’autres, etc. Newton n’imaginait pas d’univers multiples, mais il admettait l’addition illimitée des vitesses, ce qui ouvrait la possibilité d’une immobilité absolue sans cesse reculée à mesure de la découverte de nouveaux espaces. Newton prenait notre univers comme référence ultime, ce qui revenait à choisir arbitrairement celui-ci comme référentiel commun. L’impossibilité de dépasser la vitesse de la lumière dans notre univers nous donne un repère absolu, justifiant a posteriori le choix de Newton. Bien sûr le repère idéal devrait être l’immobilité absolue, mais notre univers est en expansion et tout y est en mouvement. Pas de repère absolument immobile donc, mais dépassement de l’objection de régression à l’infini. La notion de mouvement absolu prend un peu plus de consistance et il devient possible de concevoir une immobilité théorique à l’échelle de l’univers, même si elle ne peut être observée. A défaut de pouvoir calculer la vitesse absolue d’un corps, il est possible de savoir lequel de deux corps est le plus rapide par les effets de la vitesse sur l’écoulement du temps. Bien sûr, la symétrie des observations interdit de constater ces effets pendant la phase de mouvement inertiel, mais si deux observateurs, en mouvement relatif pendant un voyage, se retrouvent à l’arrivée sur le même référentiel, ils pourront comparer leurs âges et constater un écart. Nous allons illustrer tout cela avec l’histoire des jumeaux de Langevin.

Deux effets relativistes bien distincts.

Selon Einstein : « Des évènements qui sont simultanés par rapport à la voie ferrée ne sont pas simultanés par rapport au train et inversement (relativité de la simultanéité). Chaque corps de référence (système de coordonnées) a son temps propre ; une indication de temps n’a de sens que si l’on indique le corps de référence auquel elle se rapporte ». Ce texte, dont nous avons déjà cité la première partie, fait le lien entre les effets de la relativité de la simultanéité et la mesure du temps dans chaque référentiel.

La démonstration d’Einstein est la suivante :

• On avait, depuis toujours, admis qu’une indication de temps avait une valeur absolue, or la relativité de la simultanéité montre que la durée entre événements peut être perçue différemment par des observateurs en mouvement.
• Rien ne s’oppose donc à admettre que la durée soit différente au bord de la voie et dans le train.

Einstein ne dit pas que ce qui affecte le temps dans ces deux hypothèses est de même nature, mais seulement que l’abandon du caractère absolu du temps permet d’accepter qu’il s’écoule plus lentement à bord d’un référentiel en mouvement.  De fait, dans le cas de la relativité de la simultanéité, le temps est la durée mesurée entre deux évènements (voir les schémas ci dessous) :

• Soit l’écart temporel entre deux évènements distants (schéma de gauche),
• Soit la durée d’un même événement ou sa fréquence (schéma de droite)

Le texte d’Einstein est ambigu, car il désigne par l’expression « temps propre » ce qui n’est qu’un effet d’observation. En relativité de la simultanéité (qui est en fait une relativité de l’écart de réception de signaux), il n’y a pas de ralentissement des horloges, mais variation de la vitesse relative du signal lumineux en fonction du mouvement. Ceci est bien connu dans le cas de l’effet Doppler sonore : si vous éloignez de la source du signal, le son est plus grave, car la fréquence de réception s’étire. C’est l’inverse en cas de rapprochement. Bien sûr, ce ne peut être le cas avec la lumière, puisque sa vitesse étant invariante, elle ne peut être accélérée. Certes, mais c’est précisément le ralentissement temporel qui annule l’effet Doppler. Dans le cas de la lumière, la relativité de la simultanéité et celle du rythme temporel ne vont pas l’une sans l’autre.

Deux effet relativistes indissociables

La relativité de la simultanéité est un simple effet d’observation dû à l’addition des vitesses, qui donne à la lumière une vitesse calculée plus ou moins élevée en fonction du mouvement des observateurs. La dilatation temporelle est un effet réel affectant le temps de l’observateur qui se meut, annulant les effets apparents de la variation de la vitesse de la lumière en fonction du mouvement. L’ambiguïté du texte d’Einstein, qui semble confondre les deux effets, a conduit bon nombre de commentateurs de sa théorie à assimiler les effets de ralentissement temporel et de contraction des règles à un simple effet d’observation, sans écouter l’auteur qui n’a cessé d’affirmer le contraire.

Il faut distinguer entre la relativité de la simultanéité et la relativité temporelle (dilatation du temps), la seconde ne peut en effet découler de la première. Cependant, les deux effets sont inséparables et sont pris en compte dans la transformation de Lorentz, permettant de passer d’un référentiel à un autre se mouvant à une vitesse différente.

L’effet Doppler, qui est une forme de la relativité de la simultanéité, fait également l’objet d’un aménagement spécifique lorsqu’il s’agit de la lumière et non plus du son. On y ajoute le facteur de Lorentz pour tenir compte de la dilatation temporelle (effet doppler lumineux), ce qui a pour effet de compenser l’effet asymétrique de l’effet Doppler.

Longueurs et distances

Un scientifique ne peut étudier que ce qui est mesurable. Le temps comme l’espace n’ont pour lui de signification que s’il peut les représenter par des nombres. Le temps est donc pour lui de la durée et l’espace de la distance. Reste à savoir qui mesure quoi et comment. Le temps se mesure avec une horloge près de soi, les longueurs avec une règle tenue à la main et les distances par le temps que met un signal lumineux à nous parvenir. Chacun, regardant un autre se mouvant relativement à lui, constate que le temps y est ralenti et les longueurs contractées. Ceci est conforme au principe classique de relativité : les situations sont symétriques. Il y a cependant une différence, car leurs mesures des distances diffèrent, elles sont plus courtes pour le plus rapide. D’où vient donc cet écart ?

Kip S. Thorne, affirme :« La longueur d’un objet et le cours du temps sont différents dans différents référentiels. Mon temps diffère du vôtre si je me déplace par rapport à vous, et mon espace diffère du vôtre »[1]. Dans cet extrait, il est d’abord question de la longueur d’un objet et du temps, puis de l’espace et du temps, la longueur étant ainsi assimilée à l’espace, or il s’agit de deux choses différentes, ou plutôt de la même chose mesurée différemment. Même si le passager du mobile abandonne sa règle pour mesurer la longueur de son référentiel avec un signal lumineux, le ralentissement de son horloge et son mouvement l’empêcheront de constater la contraction de sa longueur. En effet, à son bord, les extrémités de son référentiel se déplacent avec lui, si bien que son mouvement (inertiel) est indécelable en interne. S’il observe un objet lointain, la vitesse de déplacement de celui-ci et du passager qui l’observe ne sont pas coordonnées et leur vitesse relative est observable.

Si la lumière se propageait instantanément d’un bout à l’autre de l’univers, tous les observateurs seraient informés simultanément d’un événement, quel que soit leur distance et leur mouvement. Tous seraient d’accord sur la simultanéité d’événement distants. Ce sont les conditions d’observation, c’est à dire la vitesse limitée de la lumière, qui empêchent qu’il en soit ainsi.

La relativité de la simultanéité peut être exprimée comme suit :

Chaque observateur, selon son référentiel, a une appréciation différente de la chronologie d’évènements distants. Ce qui est simultané pour l’un ne l’est pas pour l’autre.

L’exemple donné par Einstein est le suivant :

Supposons un train très long se déplaçant à vitesse constante relativement à la voie. Deux signaux qui sont simultanés par rapport à la voie sont-ils également simultanés par rapport au train ? La réponse est négative. Les signaux émis à chaque bout d’un quai (x) étant reçus simultanément par un observateur (A) placé au milieu de celui-ci, qu’en sera-t-il pour un observateur (B) placé à bord du train ? Même si les observateurs du quai et du train sont à égale distance de chaque bout du quai au moment de l’émission des signaux, l’observateur du quai les recevra simultanément alors que celui du train les recevra successivement, car il se dirige vers le lieu d’émission du signal E₂ et s’éloigne de celui du signal E₁.

Il en irait de même pour deux observateurs immobiles entre eux, mais placés différemment. C’est l’observateur le plus proche d’un évènement qui en a connaissance le premier. 

Sachant que les évènements observés sont indépendants des observateurs, la différence d’appréciation de la chronologie de leur survenance ne peut être qu’un effet d’observation. Einstein nous en donne d’ailleurs l’explication : cela est dû au mouvement relatif des observateurs et à la vitesse limitée de la lumière. En réalité, dans l’exemple d’Einstein, les observateurs ne tiennent pas compte de leur mouvement ou l’ignorent. Si celui du train se sait en mouvement et connaît sa vitesse relativement à la voie, il peut calculer la correction nécessaire pour connaître la chronologie des réceptions par l’observateur du quai. Tout repose sur le choix du référentiel considéré comme immobile.

Il en irait de même pour deux observateurs immobiles entre eux, mais placés différemment. C’est l’observateur le plus proche d’un évènement qui en a connaissance le premier. 

Sachant que les évènements observés sont indépendants des observateurs, la différence d’appréciation de la chronologie de leur survenance ne peut être qu’un effet d’observation. Einstein nous en donne d’ailleurs l’explication : cela est dû au mouvement relatif des observateurs et à la vitesse limitée de la lumière. En réalité, dans l’exemple d’Einstein, les observateurs ne tiennent pas compte de leur mouvement ou l’ignorent. Si celui du train se sait en mouvement et connaît sa vitesse relativement à la voie, il peut calculer la correction nécessaire pour connaître la chronologie des réceptions par l’observateur du quai. Tout repose sur le choix du référentiel considéré comme immobile.

Sur la notion d’évènement

Selon Einstein (in La relativité) : « Des évènements qui sont simultanés par rapport à la voie ferrée ne sont pas simultanés par rapport au train et inversement (relativité de la simultanéité) ». Ce texte introduit la confusion entre l’émission et la réception des signaux lumineux, alors même que Einstein fonde la relativité de la simultanéité sur la non-instantanéité    de l’information par la lumière, donc sur la distanciation entre l’émission et la réception d’un signal lumineux. Pour être exacte la formulation aurait dû être la suivante : « Des événements qui sont reçus simultanément sur la voie ne sont pas reçus simultanément à bord du train ».

L’ambiguïté du texte d’Einstein a conduit les commentateurs à y voir l’affirmation d’une divergence de simultanéités des évènements. Pourtant, si l’on tient compte du temps de transmission de l’information, la survenance de l’événement ne peut être que le moment de l’émission et non celui de la réception, qui est un autre événement, d’ailleurs propre à chaque observateur. La relativité de la simultanéité n’est que le constat de la différence de réception d’évènements distants selon les observateurs, en fonction de leur mouvement, c’est à dire un effet d’observation. Si l’on considérait que l’événement est l’émission du signal et qu’il y a autant de chronologies des émissions que d’observateurs, cela impliquerait qu’il n’y ait pas une, mais une infinité de réalités.

Pour confondre l’événement et ce qu’on en voit, il faudrait que la transmission de l’information soit instantanée. Depuis 1676[1], nous savons que la vitesse de la lumière est limitée, ce qui rend impossible la simultanéité de la survenance et de la connaissance d’un événement distant. Newton le savait aussi, mais n’en avait tiré aucune conséquence sur la notion de simultanéité, car il se plaçait toujours dans le cadre d’un référentiel commun étendu à l’univers. En admettant de se placer dans les référentiels propres à chaque observateur, sans tenir compte de la vitesse limitée de la lumière, on aboutit à considérer qu’un événement survient à des instants différents selon les observateurs, alors qu’il s’agit seulement de la connaissance de cet événement par les observateurs du fait de la lumière qui en émane.

Si nous admettons que la vitesse de la lumière est limitée et la même pour tous les observateurs, ce qui est le fondement de la théorie de la relativité restreinte, alors il n’y a plus de discordance des temps présents, puisque celui-ci est inconnaissable à distance. Pour savoir si deux évènements distants ont été simultanés dans le passé, il faut connaître l’écart de temps de la réception par l’observateur, ce qui ne pose pas de problème, mais aussi la distance à laquelle se trouvaient les événements émetteurs au moment de l’émission et la vitesse relative entre l’observateur et les émetteurs. La difficulté est que ces distances et cette vitesse sont difficiles à établir hors d’un référentiel commun. Faute de connaître sa vitesse, l’observateur va se considérer comme immobile.

[1] C’est l’astronome danois Ole Römer (1644-1710) qui effectua la première détermination de la vitesse de la   lumière par une méthode astronomique en 1676.

Observation, science et réalité

Rappelons que nous sommes à l’intérieur de l’univers et qu’il nous est impossible de savoir qui se meut réellement, ou plus exactement nous sommes dans l’impossibilité de déterminer la vitesse propre absolue des corps en mouvement (relativité du mouvement). En conséquence, si plusieurs observateurs ont une vision différente du monde qui les entoure, il est impossible d’en privilégier un plutôt qu’un autre. Toutes les observations sont recevables, par défaut.

Au-delà du système solaire, dont le soleil est la référence fixe, il est difficile de trouver un système de référence commun, si bien que chaque observateur est fondé à se considérer comme immobile par rapport à un événement lointain, sans qu’il soit possible d’en privilégier aucun. Des événements qui sont perçus comme simultanés par un observateur ne le sont pas pour d’autres (relativité de la simultanéité).

Nous ne pouvons savoir ce qui se passe présentement dans l’univers, car il faut du temps pour que l’information portée par la lumière nous parvienne. Nous ne pouvons pas non plus reconstituer ce qu’était réellement l’univers à un moment choisi arbitrairement dans le passé, car les observations d’événements anciens diffèrent selon les observateurs en raison de leur place et de leur mouvement. En effet, un corps en mouvement fuit devant les signaux émis derrière lui et abrège le parcours des signaux émis devant vers lesquels il se dirige, si bien que sa perception de la chronologie des émissions en est modifiée.

Relativité de la simultanéité et relativité temporelle

De la relativité de la simultanéité, Einstein conclut que chaque corps de référence a son temps propre, ce qui permet de passer au ralentissement des horloges, exposé par la suite. Ce sont pourtant deux mécanismes différents, aux origines distinctes.

Pour nous convaincre de la relativité de la simultanéité, Einstein nous explique que la vitesse de la lumière étant limitée et invariante, les mêmes signaux, reçus simultanément par un observateur, seront reçus successivement par un autre se mouvant relativement au premier. Du fait de la relativité du mouvement, il est impossible de savoir lequel dit vrai et si les signaux ont réellement été émis simultanément. En pratique, il est inutile de se poser la question, car elle n’a pas de réponse : il y a autant de simultanéités observées que d’observateurs. De quelle simultanéité s’agit-il ? De celle de la réception des signaux par les observateurs bien sûr, laquelle réception ne peut être confondue avec l’émission, car les deux ne peuvent être simultanés du fait de la vitesse limitée de la lumière émise. Emission et réception sont donc deux évènements distincts, éloignés dans l’espace et dans le temps. Or dans son texte, Einstein écrit que « des évènements qui sont simultanés par rapport à la voie ferrée ne sont pas simultanés par rapport au train », sans autre précision, ce qui semble confondre émission et réception en un seul et même évènement.

Einstein conclut que « chaque référentiel a son temps propre, une indication de temps n’a de sens que si l’on indique le corps de référence auquel il se rapporte ».  Il s’agit ici des indications concernant la chronologie d’évènements distants et non du rythme de fonctionnement de chaque horloge. Le temps de transmission des signaux dans l’espace n’a aucune incidence sur le rythme de fonctionnement interne des horloges de chacun des observateurs. Le terme temps propre, appliqué à la relativité de la simultanéité est source de confusion, car il est également et plus généralement utilisé pour désigner le rythme de fonctionnement de l’horloge tel que constaté par l’observateur placé à son côté, par opposition au temps mesuré sur cette même horloge depuis autre référentiel. Bien sûr, les deux phénomènes contribuent à la différence de la mesure du temps d’un observateur à un autre, mais dans un cas il s’agit de la propagation du signal lumineux jusqu’à l’observateur, dans l’autre du rythme auquel bat l’horloge qui mesure la durée.

La démonstration d’Einstein relève plutôt du procédé rhétorique que du raisonnement logique. Puisque chaque observateur en mouvement relatif a sa propre estimation de la chronologie, qui relève de la dimension temporelle, alors il est naturel que le rythme des horloges de chacun ait son propre rythme temporel. Non seulement ce n’est pas très convaincant, mais cela a conduit beaucoup de vulgarisateurs à chercher les origines de la dilatation temporelle dans la relativité de la simultanéité, ce qui est probablement la raison de leur attachement à un effet purement observationnel de la relativité restreinte. Le ralentissement temporel et la contraction des longueurs dans les référentiels en mouvement seraient un simple effet de perspective. J’ai personnellement longtemps cherché à faire fonctionner la relativité restreinte selon cette interprétation, mais sans succès. Même si les effets de la relativité de la simultanéité et ceux de la relativité temporelle et des longueurs sont inclus dans la même équation, il s’agit de deux mécanismes distincts.

[1]

Einstein a lui-même résumé sa théorie de la façon suivante : « La théorie de la relativité restreinte est basée sur deux suppositions fondamentales : les lois physiques sont les mêmes dans tous les systèmes de coordonnées en mouvement uniformes les unes par rapport aux autres ; la vitesse de la lumière a toujours la même valeur. De ces suppositions, pleinement confirmées par l’expérience, sont déduites les propriétés des règles et des horloges en mouvement, où la longueur des premières et le rythme des dernières changent avec la vitesse ». « Une autre conséquence de la théorie de la relativité (restreinte) est la connexion entre la masse et l’énergie. La masse est énergie et l’énergie a une masse [1]». Tout est dit, le reste n’est que commentaires et interprétations.

La relativité de la simultanéité

Dans son article fondateur de 1905, Einstein démontre tout d’abord que l’invariance de la vitesse de la lumière (et donc de l’information) a pour conséquence la relativité de la simultanéité, laquelle dépend de la vitesse à laquelle les observateurs se déplacent.

La vitesse de la lumière étant invariante, c’est à dire non accélérée par le mouvement du corps qui l’émet, l’observateur externe et le passager du mobile ont nécessairement une appréciation différente de la simultanéité des évènements, en raison du temps mis par l’information à leur parvenir. L’exemple donné par Einstein est celui de deux signaux émis sur une voie de chemin de fer, exactement à égale distance d’observateurs placés entre les deux émissions, l’un sur la voie et l’autre à bord d’un train lancé à grande vitesse. L’observateur de la voie considérera l’émission des signaux comme simultanée s’ils lui parviennent simultanément, alors que le passager du train, observant les mêmes signaux, sera d’un avis différent. La raison en est que le passager va au-devant du signal émis depuis l’avant du train et fuit devant le signal émis à l’arrière. Le signal arrière doit donc parcourir un trajet plus long pour atteindre le passager du train que pour parvenir à l’observateur de la voie. A l’inverse, à bord du train le trajet du signal émis devant sera plus court. De la même façon, les signaux perçus comme simultanés par le passager du train ne le seront pas pour l’observateur de la voie. Ce qui est simultané pour l’un ne l’est pas pour l’autre, de ce point de vue, les situations sont symétriques. Sans les effets relativistes, la symétrie ne serait cependant pas totale, car si chaque observateur mesure le temps que met un signal pour faire l’aller-retour du centre vers les extrémités de son propre référentiel, celui du train trouverait que son signal met un temps plus long pour faire le trajet. En contractant le train dans le sens du mouvement et en étirant le temps à son bord, la symétrie est rétablie : le passager du train ne constate rien d’anormal, la vitesse du signal lumineux étant toujours de 300 000 km/s (les km sont plus courts et les secondes plus longues).

Le ralentissement temporel et la contraction des longueurs des corps en mouvement La relativité de la simultanéité montre que des observateurs se mouvant à des vitesses différentes peuvent être en désaccord sur l’écart de temps pouvant séparer deux évènements.  Rien ne s’oppose alors, nous dit Einstein, à ce que le temps soit une donnée locale, variable en fonction de la vitesse. Si l’on admet cela, il ne reste qu’à adapter les formules mathématiques par lesquelles on passe d’un référentiel à un autre, de telle façon que la vitesse de la lumière y soit invariante.

Einstein démontre que cela passe par l’introduction des effets de la relativité de la simultanéité et de la transformation de Lorentz dans les coordonnées de temps et de longueur de la transformation de Galilée. La loi de composition des vitesses est adaptée de telle façon que la vitesse propre d’un corps transporté est ralentie à mesure que celle du transporteur augmente. Les conséquences en sont un ralentissement temporel et une contraction des longueurs constatées par les observateurs externes. Einstein ne donne pas d’explication sur la nature du phénomène : réalité ou illusion. Dans son article de 1905, Einstein n’imaginait cependant pas un seul instant que le ralentissement des horloges soit une illusion. Il écrivait : « Si nous faisons l’hypothèse que le résultat obtenu pour une ligne polygonale est également vrai pour une ligne courbe, … nous concluons qu’une horloge à balancier placée à l’équateur doit être plus lente par une trèspetite quantité qu’une autre identique placée à l’un des pôles, les autres conditions étant identiques. (§ 4 in fine) ».

Pour Einstein, l’invariance de la vitesse de la lumière en fait une limite indépassable pour tous les corps matériels. Il en résulte que la loi d’addition des vitesses doit être révisée, car les mouvements propres d’un corps s’ajoutant à la vitesse qui lui est impulsée, le résultat global pourrait être supérieur à la vitesse limite : un rayon lumineux émis depuis un corps en mouvement aurait toujours une vitesse supérieure à la vitesse limite du point de vue d’un observateur extérieur immobile ou plus lent. Il faut donc que les mouvements propres soient ralentis, jusqu’à l’immobilité totale si la vitesse impulsée atteint la vitesse limite. La transformation de Lorentz permet précisément cela.

Accélération et relativité : généralisation

Peut-on vraiment opposer le mouvement inertiel et le mouvement accéléré ? Lorsqu’il aborde les effets de la gravitation dans son exposé de la théorie de la Relativité générale, Einstein prend l’exemple de la chute libre d’un ascenseur du fait de l’attraction terrestre. Tout ce qui se trouve dans cet ascenseur est uniformément accéléré par l’effet de la gravitation, comme la cabine elle-même, ce qui produit à l’intérieur les mêmes effets qu’un mouvement inertiel en apesanteur. Sous l’effet de la gravitation, ce n’est pas la cabine de l’ascenseur qui accélère ce qu’il contient en le poussant, chaque atome du contenu est accéléré directement par l’effet de la gravitation, comme la cabine elle-même. Le mouvement, accéléré ou non, n’est jamais perceptible ni mesurable en soi, ce qui est ressenti, c’est le choc entre le contenant accéléré et son contenu en mouvement inertiel plus lent. Ce que ressent le passager d’un référentiel propulsé par un moteur, c’est n’est donc pas son mouvement, mais la poussée. Concrètement, cela va se traduire par un phénomène interne mesurable (la compression d’un ressort, par exemple) et non par comparaison spatiale avec un autre corps. Si l’on s’en tient aux coordonnées spatiales, le mouvement (déplacement) n’est toujours que relatif, même en accélération.

Einstein constatait l’équivalence entre le mouvement inertiel et le mouvement accéléré par la gravitation. Il constatait de même que la situation de l’occupant d’un ascenseur qui serait accéléré uniformément vers le haut ne diffèrerait pas de celle du terrien subissant la gravitation sur le sol de sa planète. Sur les corps transportés, l’accélération du référentiel tiré vers le haut produit les mêmes effets que la gravitation tirant les corps vers le bas avec le sol qui s’y oppose. Dans les deux cas, c’est l’opposition entre le sol et le mouvement propre des corps qui créé la pression sur ceux-ci. Lorsqu’un corps de référence est en mouvement inertiel, tous les corps qu’il emporte sont mus jusqu’au cœur des atomes. Si le corps de référence accélère, il exerce une force sur les corps transportés à laquelle ceux-ci opposent leur inertie. Il en est de même des corps posés sur terre, auxquels le sol oppose une résistance.

[1] Albert EINSTEIN & Léopold INFELD : L’évolution des idées en physiques, Champs sciences, 2009.

Einstein a lui-même résumé sa théorie de la façon suivante : « La théorie de la relativité restreinte est basée sur deux suppositions fondamentales : les lois physiques sont les mêmes dans tous les systèmes de coordonnées en mouvement uniformes les unes par rapport aux autres ; la vitesse de la lumière a toujours la même valeur. De ces suppositions, pleinement confirmées par l’expérience, sont déduites les propriétés des règles et des horloges en mouvement, où la longueur des premières et le rythme des dernières changent avec la vitesse ». « Une autre conséquence de la théorie de la relativité (restreinte) est la connexion entre la masse et l’énergie. La masse est énergie et l’énergie a une masse [1]». Tout est dit, le reste n’est que commentaires et interprétations

La relativité de la simultanéité

Dans son article fondateur de 1905, Einstein démontre tout d’abord que l’invariance de la vitesse de la lumière (et donc de l’information) a pour conséquence la relativité de la simultanéité, laquelle dépend de la vitesse à laquelle les observateurs se déplacent.

La vitesse de la lumière étant invariante, c’est à dire non accélérée par le mouvement du corps qui l’émet, l’observateur externe et le passager du mobile ont nécessairement une appréciation différente de la simultanéité des évènements, en raison du temps mis par l’information à leur parvenir. L’exemple donné par Einstein est celui de deux signaux émis sur une voie de chemin de fer, exactement à égale distance d’observateurs placés entre les deux émissions, l’un sur la voie et l’autre à bord d’un train lancé à grande vitesse. L’observateur de la voie considérera l’émission des signaux comme simultanée s’ils lui parviennent simultanément, alors que le passager du train, observant les mêmes signaux, sera d’un avis différent. La raison en est que le passager va au-devant du signal émis depuis l’avant du train et fuit devant le signal émis à l’arrière. Le signal arrière doit donc parcourir un trajet plus long pour atteindre le passager du train que pour parvenir à l’observateur de la voie. A l’inverse, à bord du train le trajet du signal émis devant sera plus court. De la même façon, les signaux perçus comme simultanés par le passager du train ne le seront pas pour l’observateur de la voie. Ce qui est simultané pour l’un ne l’est pas pour l’autre, de ce point de vue, les situations sont symétriques. Sans les effets relativistes, la symétrie ne serait cependant pas totale, car si chaque observateur mesure le temps que met un signal pour faire l’aller-retour du centre vers les extrémités de son propre référentiel, celui du train trouverait que son signal met un temps plus long pour faire le trajet. En contractant le train dans le sens du mouvement et en étirant le temps à son bord, la symétrie est rétablie : le passager du train ne constate rien d’anormal, la vitesse du signal lumineux étant toujours de 300 000 km/s (les km sont plus courts et les secondes plus longues).

Le ralentissement temporel et la contraction des longueurs des corps en mouvement

La relativité de la simultanéité montre que des observateurs se mouvant à des vitesses différentes peuvent être en désaccord sur l’écart de temps pouvant séparer deux évènements.  Rien ne s’oppose alors, nous dit Einstein, à ce que le temps soit une donnée locale, variable en fonction de la vitesse. Si l’on admet cela, il ne reste qu’à adapter les formules mathématiques par lesquelles on passe d’un référentiel à un autre, de telle façon que la vitesse de la lumière y soit invariante.

Einstein démontre que cela passe par l’introduction des effets de la relativité de la simultanéité et de la transformation de Lorentz dans les coordonnées de temps et de longueur de la transformation de Galilée. La loi de composition des vitesses est adaptée de telle façon que la vitesse propre d’un corps transporté est ralentie à mesure que celle du transporteur augmente. Les conséquences en sont un ralentissement temporel et une contraction des longueurs constatées par les observateurs externes. Einstein ne donne pas d’explication sur la nature du phénomène : réalité ou illusion. Dans son article de 1905, Einstein n’imaginait cependant pas un seul instant que le ralentissement des horloges soit une illusion. Il écrivait : « Si nous faisons l’hypothèse que le résultat obtenu pour une ligne polygonale est également vrai pour une ligne courbe, … nous concluons qu’une horloge à balancier placée à l’équateur doit être plus lente par une trèspetite quantité qu’une autre identique placée à l’un des pôles, les autres conditions étant identiques. (§ 4 in fine) ».

Pour Einstein, l’invariance de la vitesse de la lumière en fait une limite indépassable pour tous les corps matériels. Il en résulte que la loi d’addition des vitesses doit être révisée, car les mouvements propres d’un corps s’ajoutant à la vitesse qui lui est impulsée, le résultat global pourrait être supérieur à la vitesse limite : un rayon lumineux émis depuis un corps en mouvement aurait toujours une vitesse supérieure à la vitesse limite du point de vue d’un observateur extérieur immobile ou plus lent. Il faut donc que les mouvements propres soient ralentis, jusqu’à l’immobilité totale si la vitesse impulsée atteint la vitesse limite. La transformation de Lorentz permet précisément cela.

Accélération et relativité : généralisation

Peut-on vraiment opposer le mouvement inertiel et le mouvement accéléré ? Lorsqu’il aborde les effets de la gravitation dans son exposé de la théorie de la Relativité générale, Einstein prend l’exemple de la chute libre d’un ascenseur du fait de l’attraction terrestre. Tout ce qui se trouve dans cet ascenseur est uniformément accéléré par l’effet de la gravitation, comme la cabine elle-même, ce qui produit à l’intérieur les mêmes effets qu’un mouvement inertiel en apesanteur. Sous l’effet de la gravitation, ce n’est pas la cabine de l’ascenseur qui accélère ce qu’il contient en le poussant, chaque atome du contenu est accéléré directement par l’effet de la gravitation, comme la cabine elle-même. Le mouvement, accéléré ou non, n’est jamais perceptible ni mesurable en soi, ce qui est ressenti, c’est le choc entre le contenant accéléré et son contenu en mouvement inertiel plus lent. Ce que ressent le passager d’un référentiel propulsé par un moteur, c’est n’est donc pas son mouvement, mais la poussée. Concrètement, cela va se traduire par un phénomène interne mesurable (la compression d’un ressort, par exemple) et non par comparaison spatiale avec un autre corps. Si l’on s’en tient aux coordonnées spatiales, le mouvement (déplacement) n’est toujours que relatif, même en accélération.

Einstein constatait l’équivalence entre le mouvement inertiel et le mouvement accéléré par la gravitation. Il constatait de même que la situation de l’occupant d’un ascenseur qui serait accéléré uniformément vers le haut ne diffèrerait pas de celle du terrien subissant la gravitation sur le sol de sa planète. Sur les corps transportés, l’accélération du référentiel tiré vers le haut produit les mêmes effets que la gravitation tirant les corps vers le bas avec le sol qui s’y oppose. Dans les deux cas, c’est l’opposition entre le sol et le mouvement propre des corps qui créé la pression sur ceux-ci. Lorsqu’un référentiel est en mouvement inertiel, tous les corps qu’il emporte sont mus jusqu’au cœur des atomes. Si le référentiel accélère, il exerce une force sur les corps transportés à laquelle ceux-ci opposent leur inertie. Il en est de même des corps posés sur terre, auxquels le sol oppose une résistance.

[1] Albert EINSTEIN & Léopold INFELD : L’évolution des idées en physiques, Champs sciences, 2009.