Relativité de la simultanéité : le paradoxe de la grange

Les amateurs de paradoxes ont imaginé la situation suivante : sachant que les longueurs sont contractées par l’effet de la vitesse, peut-on enfermer brièvement un mobile, se déplaçant à une vitesse proche de celle de la lumière, dans une grange de même longueur que ledit mobile lorsqu’il était à l’arrêt. Bien entendu, les portes situées à chaque extrémité de la grange ne seraient fermées simultanément qu’une infime fraction de seconde, juste au moment où le mobile y serait entré en entier.

Selon la théorie de la relativité, le déplacement d’un corps à grande vitesse dans l’espace à pour effet de ralentir son rythme temporel et de contracter sa longueur. Réalité ou illusion ?

Si la contraction est une illusion, le mobile ne peut être contenu en entier dans la grange. Si la contraction est réelle, il n’y a aucun problème pour faire loger tout le mobile à l’intérieur de la grange pendant un court instant. Reste que, pour respecter la réciprocité des observations caractérisant le mouvement inertiel. le passager du mobile doit trouver la grange plus courte, puisque l’observateur de la grange trouve le mobile contracté.

Dès que le mobile est complètement à l’intérieur de la grange, l’entrée de son arrière actionne simultanément la brève fermeture des deux portes avant et arrière de celle-ci. Le mobile étant plus court que la longueur à parcourir, il n’a pas encore atteint la sortie.

Le passager du mobile ignore que sa longueur est contractée et que son rythme temporel est ralenti relativement aux mesures de la grange. Il considère donc que sa longueur est égale à celle qu’il aurait au repos (égale à celle de la grange). Il pense également que, placé au centre de son mobile, des signaux émis simultanément depuis ses extrémités lui parviennent simultanément, ayant la même distance à parcourir pour venir jusqu’à lui.

Cependant il n’en est rien, car le passager du mobile contracté va vers l’image de l’avant qui vient vers lui, alors qu’il fuit celle venant de l’arrière qui le rattrape. Les distances à parcourir par les images portées par la lumière ne sont donc pas égales. Il est atteint par celle de la sortie avant que celle de l’entrée ne lui parvienne.

Le passager du mobile en conclut que les brèves fermetures ne sont pas simultanées, la sortie entant réouverte avant que l’entrée ne se referme, ce qui lui permet de passer en entier dans une grange plus courte que lui. Comme, de plus, le mouvement de son chronomètre est ralenti, la durée de son passage dans la grange lui parait plus brève, ce qui la lui fait paraitre plus courte.

Le calcul montre que la réciprocité est parfaite et que la longueur de la grange vue par le mobile est exactement la même que la longueur du mobile vu depuis la grange. Pour la grange, le mobile contracté est mesuré par son temps de passage à la vitesse v, alors que pour le mobile la longueur de la grange non contractée est calculée par un temps de passage plus court à la vitesse v. La contraction de la longueur et celle du temps résultant de l’application de la même formule de Lorentz, le résultat obtenu de la longueur de chacun est exactement réciproque.

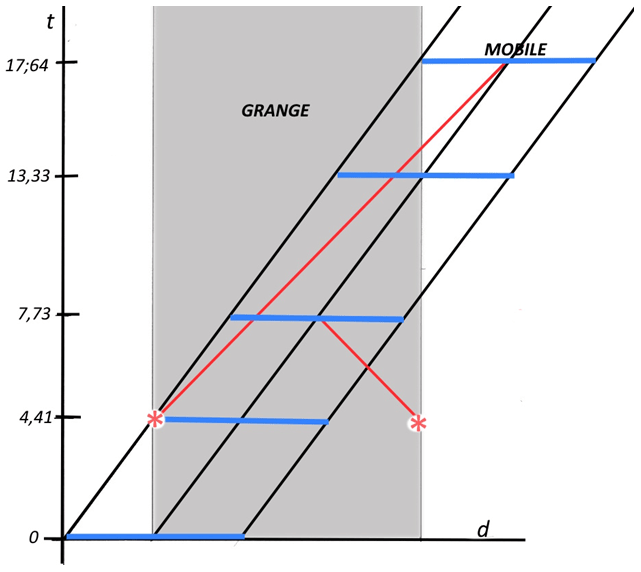
Paradoxe de la grange : calcul.

Selon la théorie de la relativité, la vitesse d’un corps a pour effet d’en ralentir le rythme temporel et d’en contacter la longueur, dans les proportions fixées par le facteur de Lorentz.

• Dans l’exemple, la vitesse étant de 0,75 fois la vitesse de la lumière, le facteur de Lorentz donne 1,5118.
• La longueur du mobile est donc réduite à 10/1,5118= 6,6146.

Alors que vu depuis la grange, les deux brèves fermetures sont simultanées, elles le sont successivement pour le passager situé au milieu du mobile (trait bleu)

• Porte devant :

Distance = (6,6146/2) + (10-6,6145) = 6,6873.

Temps = 6,6873/(1+0,75)=3,32.

• Porte derrière :

Distance = 6,6146/2=3,3073

Temps = 3,3073/(1-0,75)=13,2292.

Le passager du mobile ignore sa contraction, mais pour lui, la porte avant s’est actionnée bien après celle de l’avant, ce qui lui a largement laissé le temps de passer.

Si nous poursuivons la démonstration, le passager du mobile peut mesurer le temps mis par une de ses extrémités pour parcourir la longueur de la grange, ce qui, multiplié par sa vitesse lui donne la longueur de celle-ci.

• Temps (pour l’arrière) = 10/0.75=13,33.
• Ce qui à son horloge plus lente donne = 13,33/,.5118=8,8195.
• Longueur =8,8195x 0,75=6,6146.

Pour le passager du mobile, c’est la grange qui est la plus courte !

L’illusion de symétrie par la dissymétrie des effets relativistes

Si les effets relativistes sont réels et n’affectent que le référentiel en mouvement (ou plus exactement sont plus prononcés à bord du référentiel le plus rapide) l’observateur s’y trouvant devrait constater l’effet inverse chez le plus lent. Ceci romprait la symétrie, mais il n’en est rien, ce qui conforte ceux qui pensent que les effets relativistes sont une illusion. Les observateurs étant en mouvement relatif, l’un comme l’autre ne peut effectuer des mesures qu’en se fiant à l’information que lui transmet la lumière. Ni l’un ni l’autre ne peut lire l’heure sur une horloge lui faisant face en permanence, ni mesurer la longueur de l’autre en utilisant un mètre tenu à la main. L’observateur le plus rapide se considère comme immobile et sous-estime la distance parcourue par les signaux lumineux qu’il reçoit. Ne se sachant pas contracté, il surestime sa longueur réelle. Enfin, son horloge étant ralentie, il sous-estime la distance qu’ont dû parcourir les signaux lumineux qu’il reçoit. Ce n’est donc pas aussi simple qu’il peut y paraître de prime abord. La meilleure solution est de faire les calculs (voir les calculs ci-dessus).

Cela peut être démontré d’une autre façon. Supposons deux corps de même longueur au repos (longueur = d), dont l’un (B) est en mouvement à la vitesse v relativement à l’autre (A) immobile. La longueur de B est contractée du facteur γ du fait de sa vitesse (d_b = d / γ) et son horloge ralentie de même (t_b= t / γ). Sachant que la longueur (d) est égale à la vitesse multipliée par le temps de défilement (d=vxt), chacun mesure le temps de défilement de l’autre à sa propre horloge (t=d/v).

L’observateur immobile (A) mesure le corps comprimé (d/ γ) avec son horloge non ralentie :

Si            t=d/v  et   d_b=d/γ  
alors   t_a=d_b/v=(d/γ)/v 
donc      d_b=t_axv=((d/γ)/v)xv= d/γ

L’observateur mobile (B) mesure le corps non comprimé avec son horloge ralentie (t/γ) :

Si            t=d/v  et  t_b=t/γ
alors       t_b=t/γ=(d/v)/γ      
donc   d_a=t_bxv=((d/v)/ γ)xv= d/γ

Ainsi, la symétrie ne résulte pas d’un effet miroir dû à la relativité du mouvement, mais au fait que les effets relativistes affectent dans les mêmes proportions les mesures effectuées par chacun des observateurs. Cependant, les formules de calcul de deux référentiels en mouvement relatif donnant le même résultat, elles peuvent être échangées sans inconvénient, d’où l’impression d’effet miroir : une seule formule suffisant pour faire décrire ce que voit chaque observateur.

Limites de la symétrie

Pour Galilée, la symétrie entre les mesures effectuée par deux observateurs en mouvement relatif est limitée aux expériences physiques effectuées par chacun dans son propre référentiel. Lorsque chaque observateur regarde ce qui se passe chez l’autre, l’expérience est étendue hors du référentiel de l’observateur. Nous avons vu que chacun observe le même ralentissement (ou accélération) temporel et la même contraction des longueurs. Ils ne peuvent cependant savoir que leurs mesures sont identiques qu’à la condition d’échanger leurs informations. Si ces informations s’étendent à autre chose qu’à ce qui se passe à l’intérieur du référentiel de chacun, la symétrie s’effondre.

Se mouvant à des vitesses différentes, deux observateurs ne peuvent avoir la même appréciation de la chronologie des évènements distants. Ceci résulte de la relativité de la simultanéité. Dans l’histoire de la grange (chapitre précédent), le constat de la contraction de l’autre est réciproque, mais les observateurs sont en désaccord sur la chronologie du mouvement des portes. La relativité de la simultanéité exclut la symétrie totale.

Dans l’histoire des jumeaux de Langevin, nous avons également des observation réciproques symétriques. Remarquons toutefois que si le temps est ralenti à l’aller, conformément à ce que prévoit la théorie de la relativité, il est accéléré au retour, ce qui n’est pas conforme. Observations réciproques donc, mais de durées différentes. Pour le voyageur, l’aller et le retour sont de même durée (1 an dans chaque sens), alors qu’ils sont de durées très différentes pour le terrien (200 jours pour l’aller et 2 jours pour le retour). Nous seulement la symétrie n’est pas totale, mais, de plus, il est possible de dire qui se meut ; car à vitesse constante, l’aller et le retour sont nécessairement de longueurs égales.

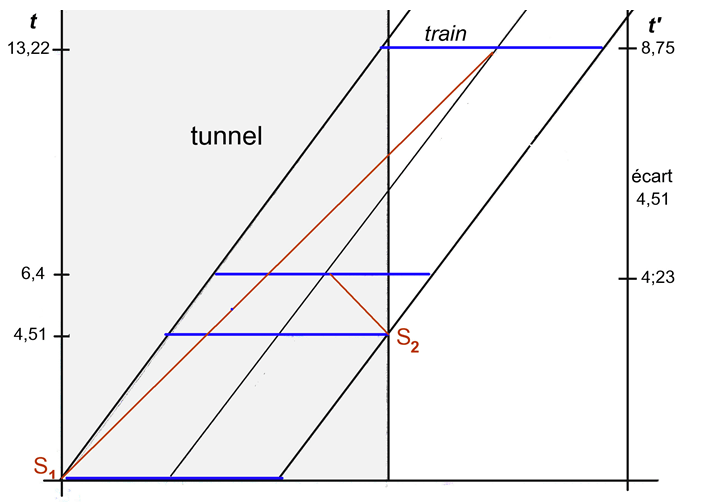
Symétrie des observations entre référentiels inertiels : la contraction des longueurs

Un train, de longueur 10 d à l’arrêt, passe sous un tunnel de même longueur à la vitesse
de 0,75 c.

Lorsque le train est entièrement entré dans le tunnel, un signal S₁ est émis et un signal S₂ lorsque l’avant du train atteint la sortie.

L’observateur placé au milieu du tunnel peut mesurer l’écart temporel entre les deux signaux pour en déduire la longueur du train dont il connaît la vitesse.

Pour γ = 1,5118, la longueur du train en mouvement est de 10 / 1,5118 = 6,61 d ,

Lorsque le train est totalement entré dans le tunnel, pour atteindre la sortie, il lui reste à, parcourir : 10 = 6,61 = 3,38 d., parcourus en 3.38 / 0,75 = 4, 51 t.

L’observateur du tunnel peut faire le calcul suivant : 

Distance parcourue en 4,51 t à 0,75 c = .3,38 d,

Longueur du train : 10 – 3,38 = 6,61 d.

Pour l’observateur placé au milieu du train (à 6,61 / 2 =  3,30 d) les signaux seront reçus :

Pour S₁ : 3,30 / (1 – 0,75) = 13,23 t après l’entrée totale dans le tunnel.

Pour S₂ , émis à +  4,41 t :  4,41 + (3,30 /( 1 – 0,75))  = 6,40 t après l’entrée totale..

Il peut en conclure que S₁ a été émis 13,23 – 6,40 = 6,82 t après S₂.

Cet écart est la conséquence de la relativité de la simultanéité.

Comme son horloge est plus lente, cet écart sera pour lui de : 6,82 / 1,5118 = 4,51 t.

Entre les deux signaux, le train a parcouru : 4,51 x 0.75 = 3,38 d,

Longueur du train : 10 – 3,38 = 6,61 d.

La symétrie des observations est parfaitement respectée, grâce aux effets relativistes

Symétrie des observations entre référentiels inertiels : la contraction des longueurs

Un train, de longueur 10 d à l’arrêt, passe sous un tunnel de même longueur à la vitesse
de 0,75 c.

Lorsque le train est entièrement entré dans le tunnel, un signal S₁ est émis et un signal S₂ lorsque l’avant du train atteint la sortie.

L’observateur placé au milieu du tunnel peut mesurer l’écart temporel entre les deux signaux pour en déduire la longueur du train dont il connaît la vitesse.

Pour γ = 1,5118, la longueur du train en mouvement est de 10 / 1,5118 = 6,61 d ,

Lorsque le train est totalement entré dans le tunnel, pour atteindre la sortie, il lui reste à, parcourir : 10 = 6,61 = 3,38 d., parcourus en 3.38 / 0,75 = 4, 51 t.

L’observateur du tunnel peut faire le calcul suivant : 

Distance parcourue en 4,51 t à 0,75 c = .3,38 d,

Longueur du train : 10 – 3,38 = 6,61 d.

Pour l’observateur placé au milieu du train (à 6,61 / 2 =  3,30 d) les signaux seront reçus :

Pour S₁ : 3,30 / (1 – 0,75) = 13,23 t après l’entrée totale dans le tunnel.

Pour S₂ , émis à +  4,41 t :  4,41 + (3,30 /( 1 – 0,75))  = 6,40 t après l’entrée totale..

Il peut en conclure que S₁ a été émis 13,23 – 6,40 = 6,82 t après S₂.

Cet écart est la conséquence de la relativité de la simultanéité.

Comme son horloge est plus lente, cet écart sera pour lui de : 6,82 / 1,5118 = 4,51 t.

Entre les deux signaux, le train a parcouru : 4,51 x 0.75 = 3,38 d,

Longueur du train : 10 – 3,38 = 6,61 d.

La symétrie des observations est parfaitement respectée, grâce aux effets relativistes