Pour Langevin il n’y a aucun paradoxe. Pour lui, son exemple (qui ne met pas en scène des jumeaux) est parfaitement conforme à la théorie de la Relativité restreinte.

La vitesse choisie pour le boulet est inférieure d’un vingt millièmes à la vitesse de la lumière de façon constante, si bien qu’en appliquant la transformation de Lorentz, 1’année passée dans le boulet équivaut à 100 années sur terre :

                                                    

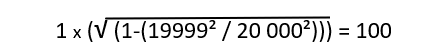
Le boulet s’éloignant pendant 1 an (temps propre), puis revenant à son point de départ, le voyage total sera évalué de 2 ans dans la fusée et de 200 ans sur terre.

Un observateur terrestre assistera au demi-tour du boulet (instantané pour ne pas compliquer les choses) au bout de 199,99 ans, la vitesse de la lumière étant 1,00005 fois plus rapide que celle de la fusée :

Vitesse lumière / vitesse boulet = 1,00005

le signal d’arrivée est émis 100 ans après le départ de la terre

il met : 100 ans / 1,00005 = 99,99 ans pour arriver à la terre,

Il sera donc reçu par la terre : 100+99,99=199,99 ans après le départ du boulet.

Le boulet sera de retour sur terre au bout de deux ans selon le temps mesuré à son bord (temps propre) et de 200 ans selon les mesures terriennes (temps impropre). Sachant que le signal de demi-tour est parvenu à la terre 199,99 ans après le départ du boulet (soit 72998 jours sans tenir compte des années bissextiles) et le retour effectif sur terre 200 ans après (soit 73000 jours), le voyage de retour sera évalué à la différence par l’observateur terrestre, soit :

73000 – 72998 = 2 jours

et le voyageur a vieilli de 2 ans quand la terre a vieilli de 2 siècles.

« Pendant qu’ils s’éloigneront l’un de l’autre avec une vitesse voisine de celle de la lumière, chacun d’eux semblera à l’autre fuir devant les signaux électromagnétiques ou lumineux qui lui sont envoyés, de sorte qu’il mettra un temps très long pour recevoir les signaux émis pendant un temps donné. Le calcul montre ainsi que chacun d’eux verra vivre l’autre deux cents fois plus lentement qu’à l’ordinaire. Pendant l’année que durera pour lui ce mouvement d’éloignement, l’explorateur ne recevra de la Terre que des nouvelles des deux premiers jours après son départ ; pendant cette année il aura vu la Terre accomplir les gestes de deux jours. »

Pour calculer la différence de temps de trajet propre à chaque référentiel, Langevin utilise la transformation de Lorentz. Ensuite, ses calculs prennent en compte les vitesses d’éloignement et de rapprochement entre la terre et le boulet et de leur effet sur la transmission de l’information (effet Doppler) :

Si v/c = 0,99995, alors 1 seconde est perçue comme durant 1 + 0,99995 = 1.99995 seconde par l’effet de l’éloignement.

Au final, le facteur de dilatation temporelle étant de 100, une seconde sera perçue 1.99995 x 100 = 199,995, donc s’écoulant près de 200 fois plus lentement. Chacun verra l’autre vivre 200 fois plus lentement.

« Pour comprendre la dissymétrie, il faut remarquer que la Terre mettra deux siècles à recevoir les signaux envoyés par l’explorateur pendant son mouvement d’éloignement qui pour lui dure un an : elle le verra vivre pendant ce temps dans son arche d’une vie deux cents fois plus ralentie ; elle lui verra accomplir les gestes d’un an. A la fin de ces deux siècles parviendra à la Terre la nouvelle de la rencontre du boulet avec l’étoile qui marque le commencement du voyage du retour. L’arrivée du voyageur se produira deux jours après pendant lesquels la Terre le verra vivre deux cents fois plus vite qu’à l’ordinaire ; lui verra accomplir les gestes d’une autre année pour le trouver au retour vieilli seulement de deux ans.

Ainsi la dissymétrie tenant à ce que le voyageur seul a subi, au milieu de son voyage, une accélération qui change le sens de sa vitesse et le ramène au point de départ sur la Terre, se traduit par ce fait que le voyageur voit la Terre s’éloigner et se rapprocher de lui pendant des temps égaux chacun pour lui à un an, tandis que la Terre, prévenue de cette accélération seulement par l’arrivée d’ondes lumineuses, voit le voyageur s’éloigner d’elle pendant deux siècles et revenir pendant deux jours, pendant un temps quarante mille fois plus court. »

Vitesse du boulet : v / c = 0,99995 de la vitesse de la lumière

Vu depuis la terre :

Voyage aller du boulet : 100 ans ou 36 500 jours (sans tenir compte des années bissextiles)

Distance parcourue jusqu’au point de demi-tour : 0,9995 x 100 = 99,995 années lumières

Durée de voyage du signal d’arrivée à la vitesse de la lumière : 99,995 ans ou 36498 jours

Réception du signal d’arrivée depuis le départ du boulet : 199,995 ans ou 72998,18 jours

Durée aller retour : 200 ans ou 73000 jours

Durée apparente retour : 200 – 99,995 = 0,01 ans ou 73000 – 72998,18 = 1,83 jours

Pour le terrien, le boulet semble donc s’être éloigné pendant 99,995 ans et être revenu en 1,83 jour (chiffres arrondis à 200 ans et 2 jours par Paul Langevin), tandis que pour le voyageur, la terre s’est éloignée pendant un an et, après le demi-tour du boulet, s’est rapprochée pendant une autre année. La situation des deux jumeaux n’est donc pas symétrique du fait du retour du référentiel fusée. Sans même parler de l’écart des âges, la dissymétrie des durées de l’aller et du retour vue par chacun des jumeaux suffirait à savoir lequel était en mouvement. Quelles sont les limites de la symétrie exigée dans les référentiels d’inertie ?

La preuve par l’expérience

Les rayons cosmiques, essentiellement formés de protons, interagissent avec les atomes des couches supérieures de l’atmosphère lorsqu’ils y pénètrent, produisant de nombreuses particules, notamment des pions, qui se désintègrent à leur tour rapidement, en produisant chacun un muon et deux neutrinos. Les muons se désintègrent à leur tour avec une durée de vie moyenne de 2,2 µs (microsecondes). Ayant une vitesse presque aussi élevée que celle de la lumière, soit 300 000 km/s (300 m/µs) ils devraient parcourir, en moyenne, une distance un peu supérieure à 600 m après leur création. Les muons sont en général créés à une altitude moyenne de 30 km, or beaucoup d’entre eux parviennent jusqu’au niveau de la mer. La durée de vie moyenne du muon (t) est donc bien supérieure à celle mesurée au repos, mais conforme à la dilatation temporelle prévue par la théorie de la Relativité restreinte. Ce fait a été vérifié expérimentalement dans un accélérateur de particules, avec des résultats également conformes. Si l’on en croit les partisans de l’illusion relativiste, l’allongement de la durée de vie du muon serait seulement apparent, dû à un effet de perspective ! Pour d’autres, ce serait dû au fait que dans son référentiel les distances sont plus courtes !