Il n’est pas nécessaire de comprendre ma théorie pour
en faire l’application. Max Planck : Initiations
à la physique

,
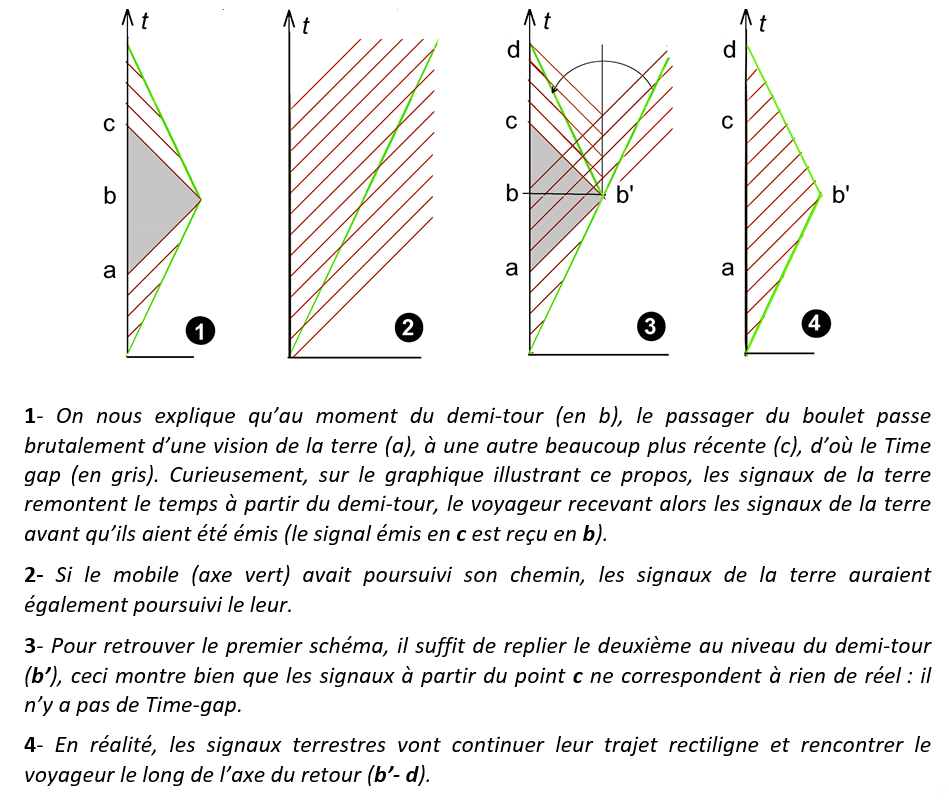
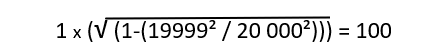Alors que Paul Langevin ne songeait qu’à illustrer la théorie de la Relativité restreinte, son histoire de voyageur en boulet est à l’origine du fameux « paradoxe des jumeaux ». Le récit initial a été quelque peu enjolivé : le boulet remplacé par un vaisseau spatial et le voyageur doté d’un jumeau resté à terre. Au retour du vaisseau, les jumeaux constatent que le voyageur est resté plus jeune : le fond de l’affaire reste donc le même.

Certains, cependant, se sont avisés que la différence des âges contredit un principe dont ils pensent qu’il est un fondement du principe de relativité : la symétrie entre référentiels inertiels. Le paradoxe n’est pas que les jumeaux vieillissent à un rythme différent, mais que cela se produise pendant le mouvement inertiel. Ils en ont conclu que le ralentissement temporel et la contraction des longueurs, prévus par la théorie de la Relativité, n’étaient que des effets d’observation et non des effets affectant réellement les corps en mouvement.

Le refus de la réalité des effets relativistes

Voici ce qu’en dit Louis de Broglie, lauréat du prix Nobel de physique en 1929 : « Il y a […] une différence essentielle entre la contraction de Lorentz-Fitzgerald et celle qui résulte, d’après Einstein, de la transformation de Lorentz. La première, en effet, était censée être une contraction réelle provoquée par le mouvement absolu du corps dans l’éther, tandis que la seconde est la contraction apparente relative au second observateur [….]. La contraction apparente des longueurs a comme complément le ralentissement apparent des horloges. […] qui résultent des nouvelles définitions de l’espace et du temps auxquelles est liée la transformation de Lorentz. […] Les raisonnements par lesquels M. Einstein a justifié sa nouvelle conception de l’espace et du temps sont souvent subtils et délicats à développer correctement, mais ils sont parfaitement solides et du point de vue logique, aucune critique sérieuse n’a pu leur être adressée[1]. En particulier, on peut parfaitement justifier le fait paradoxal que la contraction des règles et le ralentissement des horloges sont des apparences réciproques, c’est-à-dire que si deux observateurs en mouvement relatif uniforme sont munis chacun d’une règle et d’une horloge, les deux règles et les deux horloges étant de constitution identique, chacun des observateurs trouve que la règle de l’autre est plus courte que la sienne et que l’horloge de l’autre retarde sur le sienne. Si surprenante que puisse paraître au premier abord cette réciprocité, elle s’explique aisément quand on en examine avec soin la théorie, ce que naturellement nous ne pouvons faire ici ».

Einstein aurait-il été partisan du caractère seulement apparent de la contraction des longueurs et de la dilatation du temps ? Il dit explicitement le contraire : « Il est à priori évident que nous devons tirer des équations de transformation quelques renseignements sur le comportement physique des règles et des horloges ». Quelques lignes plus loin, il ajoute :  Par suite de son mouvement, l’horloge marche plus lentement que lorsqu’elle est au repos. » [2]. Les auteurs qui refusent le caractère réel des effets relativistes avancent principalement deux explications du moindre vieillissement du jumeau voyageur : les phases non inertielles du trajet (accélérations et décélérations) et le changement de référentiel au moment du demi-tour.

---

[1] La physique nouvelle et les quanta, Flammarion 1937, chapitre IV Ces commentaires montrent que Louis de Broglie ne comprenait pas vraiment la théorie développée par Einstein.

[2] Albert Einstein, La Théorie de la relativité restreinte et générale, chapitre 12, 1916, édition française Gauthier-Villars 1956).

L’explication par les accélérations et décélérations subies (phases non inertielles)

Parce qu’ils refusent la réalité des effets relativistes, de nombreux commentateurs ont prétendu résoudre le soi-disant paradoxe en sortant de la Relativité restreinte que Paul Langevin voulait précisément illustrer. Puisque la différence d’âge ne peut être le fait du mouvement inertiel, c’est donc pendant les phases non inertielles du voyage que le ralentissement temporel a eu lieu : accélération du départ, demi-tour puis freinage à l’arrivée. La symétrie des référentiels en mouvement inertiels est sauvée et comme cet argument est présenté à l’occasion d’un exposé sur la Relativité restreinte (ne traitant que des mouvements inertiels), les auteurs ne se croient pas obligés d’expliquer comment les changements d’allure produisent un tel effet. Le raisonnement est de pure logique formelle, il repose uniquement sur l’impossibilité supposée du ralentissement temporel en phase de mouvement inertiel. Quelques auteurs renvoient à la Relativité générale, qui traite de la gravitation, mais sans autre explication.

Il est plaisant cependant de constater que le moindre vieillissement du voyageur, constaté à son retour, est expliqué par des phases du voyage que Langevin avait écarté pour ne pas compliquer les calculs. En toute logique, les phases non inertielles sont déterminées par la vitesse de croisière devant être atteinte et non par la durée où celle-ci est maintenue. Si l’accélération était la cause du moindre vieillissement du voyageur, cet effet ne devrait pas être fonction de la durée du voyage, or pour obtenir la durée vécue par l’astronaute il faut diviser par γ la durée mesurée par le terrien. On voit bien que l’accélération n’est pour rien là-dedans ! La confusion vient en partie de Paul Langevin lorsqu’il fait observer que seul le voyageur ressent l’accélération au milieu du voyage, mais c’était pour souligner qu’il est le seul à constater être en mouvement et que cela rompt la symétrie des observations, le terrien ne ressentant rien de tel à l’occasion du demi-tour.

Pour apprécier l’incohérence de l’explication proposée, revenons aux calculs de Langevin.
Le voyage a duré 200 ans pour les terriens et seulement 2 ans pour le voyageur. Si le temps du voyageur s’est écoulé comme sur terre pendant la phase inertielle, la durée de celle-ci ne peut être supérieure au temps vécu par lui, c’est à dire 2 ans, ce qui suppose que le temps a été complètement suspendu pendant les accélérations et décélérations ayant durées 198 ans. Si tel était le cas, nous le saurions, il faut donc en conclure que le ralentissement temporel est progressif, ce qui ampute d’autant le temps de trajet inertiel. Les périodes d’accélération et de décélération ont donc duré entre 198 ans et 200 ans… et Langevin n’en parle pas ! C’est ridicule. Sauf à conclure que les calculs sont faux, ce que personne ne prétend, cette explication ne tient pas une seconde.

L’explication par le changement de référentiel au moment du demi-tour

L’explication concurrente consiste à dire que le demi-tour provoque une rupture de symétrie. Le voyageur saute d’un référentiel qui s’éloigne, dans un référentiel qui s’approche. La Relativité restreinte ne s’appliquerait donc pas. Reste à expliquer comment le changement de référentiel a bien pu suspendre le temps du voyageur, pendant ce qu’on appelle le « time-gap ». Pour certains, la terre aurait brusquement vieilli pendant le demi-tour. Conscients du ridicule d’une telle proposition, d’autres disent que c’est le voyageur qui a enjambé le temps qui manque, mais sans dire comment. Les partisans de cette explication peuvent se réclamer d’Einstein. Selon les propos rapportés par Charles Normann[1], d’un échange entre le physicien et Paul Painlevé en 1922, à l’objection soulevée par Painlevé de la contradiction entre le ralentissement de l’horloge mobile et la réciprocité des observations découlant de la relativité en mouvement inertiel, Einstein aurait répondu que, même en considérant seulement les phases où la vitesse du plus rapide est constante, le mobile à l’aller et le mobile au retour ne constituent pas un même système de référence, mais deux systèmes de référence différents.

Le changement de référentiel n’a pas pour effet d’avaler le temps du voyageur, mais simplement de changer les conditions d’observation. Il y a bien, en effet, rupture de symétrie, en ce sens que la réciprocité des observations suppose un mouvement relatif continu. La symétrie n’est qu’apparente et ne dure qu’autant que dure le mouvement continu. Il y a bien deux référentiels distincts en cas d’aller-retour, car, à cause de l’effet Doppler, chacun observe un ralentissement du temps chez l’autre à l’aller et une accélération au retour. Par ailleurs, en tenant compte, non pas d’observations ponctuelles, mais de la durée totale du voyage, il apparaît que le trajet du boulet de Langevin est réparti en deux parties de durée égale pour le voyageur, ce qui est normal pour un aller-retour, mais que vu depuis la terre, l’aller dure deux siècles et le retour seulement deux jours. Ces anomalies permettent de distinguer qui se déplace réellement, ce qui n’aurait pas été le cas si le mobile avait continué à s’éloigner indéfiniment. Ceci démontre bien que la symétrie constatée entre deux référentiels inertiels n’est qu’un effet d’observation, une illusion fugace.

---

[1] « Einstein expose et discute sa théorie », Revue des deux mondes, t.9, 1922, p. 129-66.

Pour Langevin il n’y a aucun paradoxe. Pour lui, son exemple (qui ne met pas en scène des jumeaux) est parfaitement conforme à la théorie de la Relativité restreinte.

La vitesse choisie pour le boulet est inférieure d’un vingt millièmes à la vitesse de la lumière de façon constante, si bien qu’en appliquant la transformation de Lorentz, 1’année passée dans le boulet équivaut à 100 années sur terre :

                                                    

Le boulet s’éloignant pendant 1 an (temps propre), puis revenant à son point de départ, le voyage total sera évalué de 2 ans dans la fusée et de 200 ans sur terre.

Un observateur terrestre assistera au demi-tour du boulet (instantané pour ne pas compliquer les choses) au bout de 199,99 ans, la vitesse de la lumière étant 1,00005 fois plus rapide que celle de la fusée :

Vitesse lumière / vitesse boulet = 1,00005

le signal d’arrivée est émis 100 ans après le départ de la terre

il met : 100 ans / 1,00005 = 99,99 ans pour arriver à la terre,

Il sera donc reçu par la terre : 100+99,99=199,99 ans après le départ du boulet.

Le boulet sera de retour sur terre au bout de deux ans selon le temps mesuré à son bord (temps propre) et de 200 ans selon les mesures terriennes (temps impropre). Sachant que le signal de demi-tour est parvenu à la terre 199,99 ans après le départ du boulet (soit 72998 jours sans tenir compte des années bissextiles) et le retour effectif sur terre 200 ans après (soit 73000 jours), le voyage de retour sera évalué à la différence par l’observateur terrestre, soit :

73000 – 72998 = 2 jours

et le voyageur a vieilli de 2 ans quand la terre a vieilli de 2 siècles.

« Pendant qu’ils s’éloigneront l’un de l’autre avec une vitesse voisine de celle de la lumière, chacun d’eux semblera à l’autre fuir devant les signaux électromagnétiques ou lumineux qui lui sont envoyés, de sorte qu’il mettra un temps très long pour recevoir les signaux émis pendant un temps donné. Le calcul montre ainsi que chacun d’eux verra vivre l’autre deux cents fois plus lentement qu’à l’ordinaire. Pendant l’année que durera pour lui ce mouvement d’éloignement, l’explorateur ne recevra de la Terre que des nouvelles des deux premiers jours après son départ ; pendant cette année il aura vu la Terre accomplir les gestes de deux jours. »

Pour calculer la différence de temps de trajet propre à chaque référentiel, Langevin utilise la transformation de Lorentz. Ensuite, ses calculs prennent en compte les vitesses d’éloignement et de rapprochement entre la terre et le boulet et de leur effet sur la transmission de l’information (effet Doppler) :

Si v/c = 0,99995, alors 1 seconde est perçue comme durant 1 + 0,99995 = 1.99995 seconde par l’effet de l’éloignement.

Au final, le facteur de dilatation temporelle étant de 100, une seconde sera perçue 1.99995 x 100 = 199,995, donc s’écoulant près de 200 fois plus lentement. Chacun verra l’autre vivre 200 fois plus lentement.

« Pour comprendre la dissymétrie, il faut remarquer que la Terre mettra deux siècles à recevoir les signaux envoyés par l’explorateur pendant son mouvement d’éloignement qui pour lui dure un an : elle le verra vivre pendant ce temps dans son arche d’une vie deux cents fois plus ralentie ; elle lui verra accomplir les gestes d’un an. A la fin de ces deux siècles parviendra à la Terre la nouvelle de la rencontre du boulet avec l’étoile qui marque le commencement du voyage du retour. L’arrivée du voyageur se produira deux jours après pendant lesquels la Terre le verra vivre deux cents fois plus vite qu’à l’ordinaire ; lui verra accomplir les gestes d’une autre année pour le trouver au retour vieilli seulement de deux ans.

Ainsi la dissymétrie tenant à ce que le voyageur seul a subi, au milieu de son voyage, une accélération qui change le sens de sa vitesse et le ramène au point de départ sur la Terre, se traduit par ce fait que le voyageur voit la Terre s’éloigner et se rapprocher de lui pendant des temps égaux chacun pour lui à un an, tandis que la Terre, prévenue de cette accélération seulement par l’arrivée d’ondes lumineuses, voit le voyageur s’éloigner d’elle pendant deux siècles et revenir pendant deux jours, pendant un temps quarante mille fois plus court. »

Vitesse du boulet : v / c = 0,99995 de la vitesse de la lumière

Vu depuis la terre :

Voyage aller du boulet : 100 ans ou 36 500 jours (sans tenir compte des années bissextiles)

Distance parcourue jusqu’au point de demi-tour : 0,9995 x 100 = 99,995 années lumières

Durée de voyage du signal d’arrivée à la vitesse de la lumière : 99,995 ans ou 36498 jours

Réception du signal d’arrivée depuis le départ du boulet : 199,995 ans ou 72998,18 jours

Durée aller retour : 200 ans ou 73000 jours

Durée apparente retour : 200 – 99,995 = 0,01 ans ou 73000 – 72998,18 = 1,83 jours

Pour le terrien, le boulet semble donc s’être éloigné pendant 99,995 ans et être revenu en 1,83 jour (chiffres arrondis à 200 ans et 2 jours par Paul Langevin), tandis que pour le voyageur, la terre s’est éloignée pendant un an et, après le demi-tour du boulet, s’est rapprochée pendant une autre année. La situation des deux jumeaux n’est donc pas symétrique du fait du retour du référentiel fusée. Sans même parler de l’écart des âges, la dissymétrie des durées de l’aller et du retour vue par chacun des jumeaux suffirait à savoir lequel était en mouvement. Quelles sont les limites de la symétrie exigée dans les référentiels d’inertie ?

La preuve par l’expérience

Les rayons cosmiques, essentiellement formés de protons, interagissent avec les atomes des couches supérieures de l’atmosphère lorsqu’ils y pénètrent, produisant de nombreuses particules, notamment des pions, qui se désintègrent à leur tour rapidement, en produisant chacun un muon et deux neutrinos. Les muons se désintègrent à leur tour avec une durée de vie moyenne de 2,2 µs (microsecondes). Ayant une vitesse presque aussi élevée que celle de la lumière, soit 300 000 km/s (300 m/µs) ils devraient parcourir, en moyenne, une distance un peu supérieure à 600 m après leur création. Les muons sont en général créés à une altitude moyenne de 30 km, or beaucoup d’entre eux parviennent jusqu’au niveau de la mer. La durée de vie moyenne du muon (t) est donc bien supérieure à celle mesurée au repos, mais conforme à la dilatation temporelle prévue par la théorie de la Relativité restreinte. Ce fait a été vérifié expérimentalement dans un accélérateur de particules, avec des résultats également conformes. Si l’on en croit les partisans de l’illusion relativiste, l’allongement de la durée de vie du muon serait seulement apparent, dû à un effet de perspective ! Pour d’autres, ce serait dû au fait que dans son référentiel les distances sont plus courtes !