Deux effets relativistes bien distincts.

Selon Einstein : « Des évènements qui sont simultanés par rapport à la voie ferrée ne sont pas simultanés par rapport au train et inversement (relativité de la simultanéité). Chaque corps de référence (système de coordonnées) a son temps propre ; une indication de temps n’a de sens que si l’on indique le corps de référence auquel elle se rapporte ». Ce texte, dont nous avons déjà cité la première partie, fait le lien entre les effets de la relativité de la simultanéité et la mesure du temps dans chaque référentiel.

La démonstration d’Einstein est la suivante :

• On avait, depuis toujours, admis qu’une indication de temps avait une valeur absolue, or la relativité de la simultanéité montre que la durée entre événements peut être perçue différemment par des observateurs en mouvement.
• Rien ne s’oppose donc à admettre que la durée soit différente au bord de la voie et dans le train.

Einstein ne dit pas que ce qui affecte le temps dans ces deux hypothèses est de même nature, mais seulement que l’abandon du caractère absolu du temps permet d’accepter qu’il s’écoule plus lentement à bord d’un référentiel en mouvement.  De fait, dans le cas de la relativité de la simultanéité, le temps est la durée mesurée entre deux évènements (voir les schémas ci dessous) :

• Soit l’écart temporel entre deux évènements distants (schéma de gauche),
• Soit la durée d’un même événement ou sa fréquence (schéma de droite)

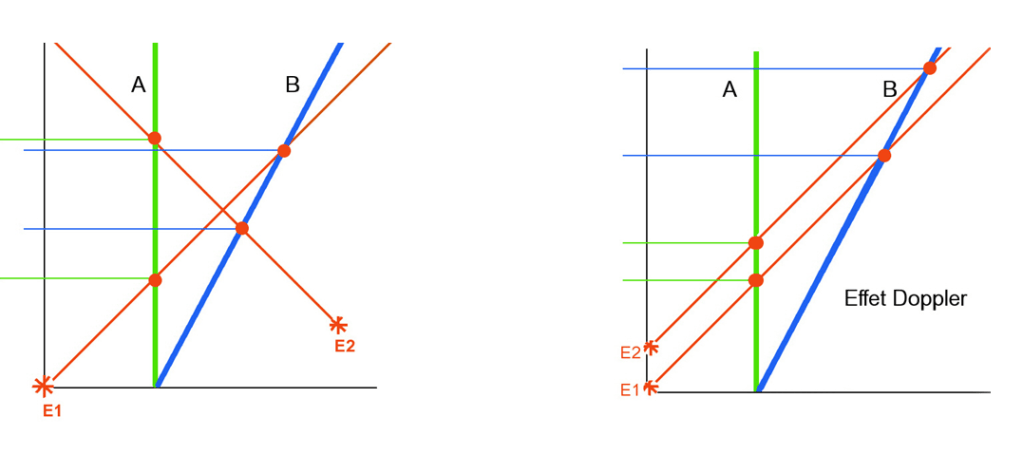
Le texte d’Einstein est ambigu, car il désigne par l’expression « temps propre » ce qui n’est qu’un effet d’observation. En relativité de la simultanéité (qui est en fait une relativité de l’écart de réception de signaux), il n’y a pas de ralentissement des horloges, mais variation de la vitesse relative du signal lumineux en fonction du mouvement. Ceci est bien connu dans le cas de l’effet Doppler sonore : si vous éloignez de la source du signal, le son est plus grave, car la fréquence de réception s’étire. C’est l’inverse en cas de rapprochement. Bien sûr, ce ne peut être le cas avec la lumière, puisque sa vitesse étant invariante, elle ne peut être accélérée. Certes, mais c’est précisément le ralentissement temporel qui annule l’effet Doppler. Dans le cas de la lumière, la relativité de la simultanéité et celle du rythme temporel ne vont pas l’une sans l’autre.

Deux effet relativistes indissociables

La relativité de la simultanéité est un simple effet d’observation dû à l’addition des vitesses, qui donne à la lumière une vitesse calculée plus ou moins élevée en fonction du mouvement des observateurs. La dilatation temporelle est un effet réel affectant le temps de l’observateur qui se meut, annulant les effets apparents de la variation de la vitesse de la lumière en fonction du mouvement. L’ambiguïté du texte d’Einstein, qui semble confondre les deux effets, a conduit bon nombre de commentateurs de sa théorie à assimiler les effets de ralentissement temporel et de contraction des règles à un simple effet d’observation, sans écouter l’auteur qui n’a cessé d’affirmer le contraire.

Il faut distinguer entre la relativité de la simultanéité et la relativité temporelle (dilatation du temps), la seconde ne peut en effet découler de la première. Cependant, les deux effets sont inséparables et sont pris en compte dans la transformation de Lorentz, permettant de passer d’un référentiel à un autre se mouvant à une vitesse différente.

L’effet Doppler, qui est une forme de la relativité de la simultanéité, fait également l’objet d’un aménagement spécifique lorsqu’il s’agit de la lumière et non plus du son. On y ajoute le facteur de Lorentz pour tenir compte de la dilatation temporelle (effet doppler lumineux), ce qui a pour effet de compenser l’effet asymétrique de l’effet Doppler.

Longueurs et distances

Un scientifique ne peut étudier que ce qui est mesurable. Le temps comme l’espace n’ont pour lui de signification que s’il peut les représenter par des nombres. Le temps est donc pour lui de la durée et l’espace de la distance. Reste à savoir qui mesure quoi et comment. Le temps se mesure avec une horloge près de soi, les longueurs avec une règle tenue à la main et les distances par le temps que met un signal lumineux à nous parvenir. Chacun, regardant un autre se mouvant relativement à lui, constate que le temps y est ralenti et les longueurs contractées. Ceci est conforme au principe classique de relativité : les situations sont symétriques. Il y a cependant une différence, car leurs mesures des distances diffèrent, elles sont plus courtes pour le plus rapide. D’où vient donc cet écart ?

Kip S. Thorne, affirme :« La longueur d’un objet et le cours du temps sont différents dans différents référentiels. Mon temps diffère du vôtre si je me déplace par rapport à vous, et mon espace diffère du vôtre »[1]. Dans cet extrait, il est d’abord question de la longueur d’un objet et du temps, puis de l’espace et du temps, la longueur étant ainsi assimilée à l’espace, or il s’agit de deux choses différentes, ou plutôt de la même chose mesurée différemment. Même si le passager du mobile abandonne sa règle pour mesurer la longueur de son référentiel avec un signal lumineux, le ralentissement de son horloge et son mouvement l’empêcheront de constater la contraction de sa longueur. En effet, à son bord, les extrémités de son référentiel se déplacent avec lui, si bien que son mouvement (inertiel) est indécelable en interne. S’il observe un objet lointain, la vitesse de déplacement de celui-ci et du passager qui l’observe ne sont pas coordonnées et leur vitesse relative est observable.

---