La cause physique du ralentissement des horloges et de la contraction des règles

Quelle est la cause du ralentissement des horloges et de la contraction des règles ? Einstein est silencieux à ce sujet. Il pose cependant la question : « Comment ? » dans l’ouvrage co-écrit avec Léopold Infield, et curieusement, il répond que « Il suit de la transformation de Lorentz, qu’un bâton se réduirait à rien… » Ainsi, la cause des effets relativistes serait une formule mathématique. Il semble bien qu’Einstein n’a pas d’explication physique du phénomène.

La théorie de la Relativité a permis de résoudre un certain nombre de problèmes et ses prédictions se sont révélées fiables. Cette théorie est donc exacte, et comme elle est fondée sur la transformation de Lorentz qui conduit à la dilatation du temps et à la contraction des règles, il faut admettre ces effets, même s’ils sont contre-intuitifs. C’est cependant un peu court comme explication. Cela revient à dire que le monde est mathématique et qu’il faut admettre toutes les conséquences d’une équation, même si on n’y comprend rien.

N’étant pas physicien, ma proposition va peut-être paraître ridicule, mais tant pis, je me lance. Partant du fait que la vitesse de la lumière ne peut être dépassée, nous devons admettre que si un atome était projeté à une vitesse proche de la lumière, la rotation ou la vibration des électrons autour du noyau serait ralentie, jusqu’à cesser totalement si la vitesse de la lumière pouvait être atteinte. A bord d’un vaisseau propulsé à une vitesse proche de celle de la lumière, tous les mouvements seraient ralentis à bord, ceux des électrons comme ceux des passagers.

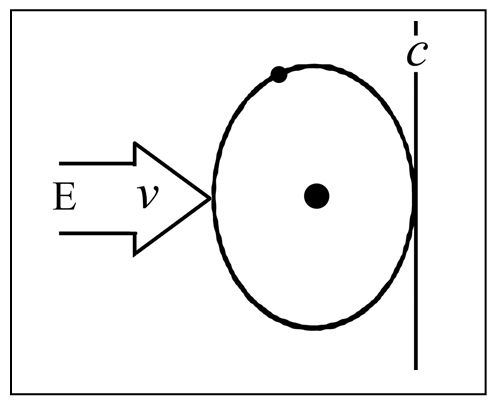
Les mouvements des électrons autour du noyau seraient parfaitement circulaires en cas d’absence de toute vitesse impulsée. L’addition de la vitesse propre des électrons et de la vitesse impulsée n’a d’effet que dans le sens du mouvement, latéralement, les vitesses ne se cumulent pas totalement. De ce fait, la course des électrons étant ralentie dans le sens du mouvement impulsé, leur orbite est aplatie et devient elliptique. Il en résulte une contraction des corps dans le sens de leur déplacement.

L’explication donnée par Einstein est que lorsqu’une impulsion est donnée à un corps pour accroître sa vitesse, cela à pour effet d’augmenter sa masse par transfert d’énergie. Plus la masse d’un corps est grande et plus il faut d’énergie pour augmenter sa vitesse, donc plus il va vite et plus l’énergie nécessaire pour encore accroître sa vitesse doit être importante. Lorsqu’un corps atteint la vitesse de la lumière, il faudrait une énergie infinie pour l’accélérer encore. En outre, un corps matériel qui atteindrait cette vitesse aurait une masse infinie.

A bord d’un corps approchant la vitesse de la lumière, la vitesse propre de son contenu est ralentie jusqu’à cesser totalement lorsque la vitesse de la lumière est atteinte, car la vitesse propre du contenu ne peut plus s’ajouter à celle du corps qui le contient. En pratique, cet arrêt ne peut être brutal, il est progressif à mesure que la vitesse du contenant s’approche de celle de la lumière.

Le phénomène de contraction des longueurs est assez proche de ce qui se passe dans les trous noirs, où la force de la gravitation contracte les atomes au point que la masse d’un tel corps céleste devient gigantesque relativement à son volume. De même, tout corps en mouvement a reçu de l’énergie pour atteindre sa vitesse, ce qui accroît sa masse et contracte sa longueur dans le sens du mouvement.

Contraction des règles et contraction des distances

Il est souvent affirmé que la contraction des distances observées par le passager du référentiel en mouvement est la conséquence de la contraction des longueurs à son bord. La contraction des longueurs est invisible pour le passager, seul l’observateur externe peut la constater. Ceci est normal, car à bord du référentiel en mouvement les longueurs sont mesurées avec des règles également contractées. Il est curieux cependant que ce passager ne puisse constater la contraction de ce qu’il mesure à son bord et constate une contraction des distances dans l’espace qui l’entoure. A l’inverse, celui qui l’observe et se dit immobile, constate la contraction des longueurs du référentiel en mouvement, sans que l’espace en soit affecté de son point de vue. La contraction des distances est un phénomène qui ne peut affecter que l’espace visible par le passager du corps en mouvement.

Le simple bon sens nous dit que l’espace de l’univers est le même pour tout le monde et que si on le mesure avec une règle contractée, le résultat doit être une plus grande distance mesurée et non une plus courte. En pratique, si les longueurs se mesurent avec une règle, les distances se mesurent avec une horloge. Cependant, si l’horloge et la règle sont semblablement affectées par les effets relativistes, comment expliquer que les mesures spatiales effectues avec une règle donnent les mêmes résultats dans les deux référentiels en mouvement relatif et pas celles effectuées avec les horloges ? La raison en est qu’avec la règle on mesure des longueurs contractées comme elle, alors qu’avec l’horloge on mesure le temps mis par la lumière à parcourir une distance et que la vitesse de la lumière est invariante, non affectée par les effets relativistes dû à la vitesse. Si le rythme de l’horloge ralentit, les distances mesurées sont plus courtes. Il s’agit donc d’un effet purement observationnel. D’ailleurs, comment pourrait-on expliquer que la vitesse aurait pour effet de contracter l’espace autour du corps qui se meut sans affecter également celui de l’observateur qui se pense immobile ?

La contraction des longueurs et la contraction des distances sont donc deux phénomènes distincts, même s’il n’y a pas d’inconvénient pratique à les confondre dans les calculs, le facteur γ étant le même pour les longueurs et pour le temps. Le seul problème est que si la contraction des longueurs à bord est réelle, on en conclut que celle de l’espace l’est également, ce qui conduit à admettre autant d’espaces que d’observateurs, ce qui n’est pas une solution très économique.

Si nous admettons que les effets relativistes ne sont pas une illusion, le ralentissement des horloges et la contraction des longueurs sont réels. Pour mesurer une distance extérieure à son référentiel, tout observateur utilise un signal lumineux. S’il émet lui-même le signal, il mesure le temps de trajet aller-retour et divise par deux. Le résultat de sa mesure est directement fonction du rythme de fonctionnement de son horloge. Deux observateurs se mouvant à des vitesses différentes seront donc en désaccord sur la mesure des distances, leurs horloges respectives battant à des cadences différentes. L’écart de mesure des distances est la conséquence directe de l’écart d’écoulement temporel et dans les mêmes proportions (facteur de Lorentz).

En pratique, il suffit d’appliquer le facteur de Lorentz à la distance mesurée pour obtenir celle calculée par un observateur en mouvement dont je connais la vitesse relative. Le résultat est exact, mais ce mode de calcul peut laisser penser que c’est l’espace qui est directement contracté dans l’univers du référentiel mobile, ce d’autant plus que cela correspond très exactement à la contraction réelle des longueurs à bord du référentiel mobile. En réalité, la contraction des longueurs n’a rien à voir dans cette affaire, seul le ralentissement temporel est en cause. Il suffit que les horloges soient plus lentes pour que les distances paraissent plus courtes, sans contraction physique réelle de l’espace.

Espace et temps sont distincts, mais pour les observateurs, ils sont intimement liés car tout écart temporel conduit à un écart de mesure des distances dans les mêmes proportions. Les théories et méthodes scientifiques devant être conformes à l’observation, il est normal que cette union observée du temps et de l’espace soit prise en compte par le physicien dans ses calculs. L’espace-temps est donc une vérité scientifique puisque c’est une réalité observationnelle, mais cela n’en fait pas pour autant la réalité physique : la contraction mesurée des distances est seulement la conséquence du ralentissement temporel.

Avec un certain enthousiasme, Minkowski a écrit que « l’espace, considéré séparément, et le temps considéré séparément, sont destinés à disparaître comme des ombres », concluant que « seule une sorte d’union des deux gardera une réalité indépendante ». De quelle réalité
s’agit-il ? Minkowski n’aurait-il pas pris ses diagrammes pour la réalité ? Ce ne sont pas l’espace et le temps qui sont liés, mais leur mesure. L’espace-temps de Minkowski est le résultat de cette union, due aux particularités de la lumière par laquelle nous parvient l’information. Ce n’est pas une description de la réalité, mais de ce que nous observons. Si nous admettons cela, la théorie de la Relativité relève du sens commun, à la seule condition d’admettre l’invariance de la vitesse de la lumière et l’impossibilité de la dépasser. La mesure des distances étant faite à l’aide d’une horloge qui bat au rythme de chacun en fonction de sa vitesse, il en résulte que chacun voit le monde à sa manière, ce qui explique pourquoi il y a autant d’espace-temps que d’observateurs se mouvant à des vitesses différentes. Dans le réel, il y à l’espace commun et des observateurs qui le mesurent avec des horloges battant à des rythmes différents et obtiennent des résultats discordants. L’observateur immobile peut appliquer le facteur de Lorentz directement à ses propres mesures de distances pour passer dans l’espace-temps du mobile observé, mais c’est une facilité qui fait oublier qu’en réalité c’est le temps seul qui est concerné. Le résultat est exact, mais si l’on pense que l’espace est contracté comme l’est la longueur du mobile, l’explication est fausse et tout devient incompréhensible. Il n’y a en effet rien à comprendre lorsque nous acceptons un résultat conforme à l’observation comme étant l’expression de la réalité, sans chercher à comprendre comment il est obtenu.

Incidences sur la notion de mouvement propre et de mouvement absolu

L’impossibilité de dépasser la vitesse de la lumière a une conséquence sur la notion de mouvement absolu. Nous avons vu que rien ne s’oppose à ce que notre univers ne soit qu’un parmi d’autres, entraînés dans un même mouvement. Il est ainsi possible d’envisager une régression à l’infini en imaginant que notre groupement d’univers n’est qu’un parmi d’autres, etc. Newton n’imaginait pas d’univers multiples, mais il admettait l’addition illimitée des vitesses, ce qui ouvrait la possibilité d’une immobilité absolue sans cesse reculée à mesure de la découverte de nouveaux espaces. Newton prenait notre univers comme référence ultime, ce qui revenait à choisir arbitrairement celui-ci comme référentiel commun. L’impossibilité de dépasser la vitesse de la lumière dans notre univers nous donne un repère absolu, justifiant a posteriori le choix de Newton. Bien sûr le repère idéal devrait être l’immobilité absolue, mais notre univers est en expansion et tout y est en mouvement. Pas de repère absolument immobile donc, mais dépassement de l’objection de régression à l’infini. La notion de mouvement absolu prend un peu plus de consistance et il devient possible de concevoir une immobilité théorique à l’échelle de l’univers, même si elle ne peut être observée. A défaut de pouvoir calculer la vitesse absolue d’un corps, il est possible de savoir lequel de deux corps est le plus rapide par les effets de la vitesse sur l’écoulement du temps. Bien sûr, la symétrie des observations interdit de constater ces effets pendant la phase de mouvement inertiel, mais si deux observateurs, en mouvement relatif pendant un voyage, se retrouvent à l’arrivée sur le même référentiel, ils pourront comparer leurs âges et constater un écart. Nous allons illustrer tout cela avec l’histoire des jumeaux de Langevin.

Deux effets relativistes bien distincts.

Selon Einstein : « Des évènements qui sont simultanés par rapport à la voie ferrée ne sont pas simultanés par rapport au train et inversement (relativité de la simultanéité). Chaque corps de référence (système de coordonnées) a son temps propre ; une indication de temps n’a de sens que si l’on indique le corps de référence auquel elle se rapporte ». Ce texte, dont nous avons déjà cité la première partie, fait le lien entre les effets de la relativité de la simultanéité et la mesure du temps dans chaque référentiel.

La démonstration d’Einstein est la suivante :

• On avait, depuis toujours, admis qu’une indication de temps avait une valeur absolue, or la relativité de la simultanéité montre que la durée entre événements peut être perçue différemment par des observateurs en mouvement.
• Rien ne s’oppose donc à admettre que la durée soit différente au bord de la voie et dans le train.

Einstein ne dit pas que ce qui affecte le temps dans ces deux hypothèses est de même nature, mais seulement que l’abandon du caractère absolu du temps permet d’accepter qu’il s’écoule plus lentement à bord d’un référentiel en mouvement.  De fait, dans le cas de la relativité de la simultanéité, le temps est la durée mesurée entre deux évènements (voir les schémas ci dessous) :

• Soit l’écart temporel entre deux évènements distants (schéma de gauche),
• Soit la durée d’un même événement ou sa fréquence (schéma de droite)

Le texte d’Einstein est ambigu, car il désigne par l’expression « temps propre » ce qui n’est qu’un effet d’observation. En relativité de la simultanéité (qui est en fait une relativité de l’écart de réception de signaux), il n’y a pas de ralentissement des horloges, mais variation de la vitesse relative du signal lumineux en fonction du mouvement. Ceci est bien connu dans le cas de l’effet Doppler sonore : si vous éloignez de la source du signal, le son est plus grave, car la fréquence de réception s’étire. C’est l’inverse en cas de rapprochement. Bien sûr, ce ne peut être le cas avec la lumière, puisque sa vitesse étant invariante, elle ne peut être accélérée. Certes, mais c’est précisément le ralentissement temporel qui annule l’effet Doppler. Dans le cas de la lumière, la relativité de la simultanéité et celle du rythme temporel ne vont pas l’une sans l’autre.

Deux effet relativistes indissociables

La relativité de la simultanéité est un simple effet d’observation dû à l’addition des vitesses, qui donne à la lumière une vitesse calculée plus ou moins élevée en fonction du mouvement des observateurs. La dilatation temporelle est un effet réel affectant le temps de l’observateur qui se meut, annulant les effets apparents de la variation de la vitesse de la lumière en fonction du mouvement. L’ambiguïté du texte d’Einstein, qui semble confondre les deux effets, a conduit bon nombre de commentateurs de sa théorie à assimiler les effets de ralentissement temporel et de contraction des règles à un simple effet d’observation, sans écouter l’auteur qui n’a cessé d’affirmer le contraire.

Il faut distinguer entre la relativité de la simultanéité et la relativité temporelle (dilatation du temps), la seconde ne peut en effet découler de la première. Cependant, les deux effets sont inséparables et sont pris en compte dans la transformation de Lorentz, permettant de passer d’un référentiel à un autre se mouvant à une vitesse différente.

L’effet Doppler, qui est une forme de la relativité de la simultanéité, fait également l’objet d’un aménagement spécifique lorsqu’il s’agit de la lumière et non plus du son. On y ajoute le facteur de Lorentz pour tenir compte de la dilatation temporelle (effet doppler lumineux), ce qui a pour effet de compenser l’effet asymétrique de l’effet Doppler.

Longueurs et distances

Un scientifique ne peut étudier que ce qui est mesurable. Le temps comme l’espace n’ont pour lui de signification que s’il peut les représenter par des nombres. Le temps est donc pour lui de la durée et l’espace de la distance. Reste à savoir qui mesure quoi et comment. Le temps se mesure avec une horloge près de soi, les longueurs avec une règle tenue à la main et les distances par le temps que met un signal lumineux à nous parvenir. Chacun, regardant un autre se mouvant relativement à lui, constate que le temps y est ralenti et les longueurs contractées. Ceci est conforme au principe classique de relativité : les situations sont symétriques. Il y a cependant une différence, car leurs mesures des distances diffèrent, elles sont plus courtes pour le plus rapide. D’où vient donc cet écart ?

Kip S. Thorne, affirme :« La longueur d’un objet et le cours du temps sont différents dans différents référentiels. Mon temps diffère du vôtre si je me déplace par rapport à vous, et mon espace diffère du vôtre »[1]. Dans cet extrait, il est d’abord question de la longueur d’un objet et du temps, puis de l’espace et du temps, la longueur étant ainsi assimilée à l’espace, or il s’agit de deux choses différentes, ou plutôt de la même chose mesurée différemment. Même si le passager du mobile abandonne sa règle pour mesurer la longueur de son référentiel avec un signal lumineux, le ralentissement de son horloge et son mouvement l’empêcheront de constater la contraction de sa longueur. En effet, à son bord, les extrémités de son référentiel se déplacent avec lui, si bien que son mouvement (inertiel) est indécelable en interne. S’il observe un objet lointain, la vitesse de déplacement de celui-ci et du passager qui l’observe ne sont pas coordonnées et leur vitesse relative est observable.

---