À la fin du XIXème siècle, on pensait que la science physique était achevée. Il restait bien quelques petits problèmes à régler, comme celui de l’incompatibilité entre la mécanique et l’électrodynamique, mais il ne faisait aucun doute que ce n’était que des détails. Einstein parvint à étendre la loi de l’invariance des lois mécaniques dans les référentiels d’inertie à l’invariance de la lumière de l’électrodynamique… et cela révolutionna la physique.
L’invariance de la vitesse de la lumière et la vaine recherche de l’éther
Lorsque nous contemplons le ciel étoilé nocturne, il nous semble voir l’état présent de l’univers, mais il n’en est rien. La lumière provenant des étoiles ne nous parvient pas instantanément, mais voyage à 300 000 km/s : l’image qui nous en parvient est donc d’autant plus ancienne que la source est plus éloignée de nous. Non seulement ce que nous contemplons n’est pas l’état présent de l’univers, mais encore les objets célestes que nous y voyons ne sont pas tous contemporains entre eux.
La lumière ne se propage pas instantanément, ce qui fait de la lumière un corps comme un autre : c’est le photon. Toutefois, selon les lois de l’électrodynamique, la vitesse de la lumière est invariable, quelle que soit la vitesse du corps qui l’émet ou celle de celui qui la reçoit. Ceci est exprimé par le postulat suivant :
La vitesse de la lumière (dans le vide) est la même dans tous les référentiels d’inertie. Elle est indépendante du mouvement de sa source ou de l’observateur.
Par analogie avec les ondes sonores, consistant en une déformation du milieu ambiant de l’air (l’espace sans air est silencieux), les physiciens ont cherché à mettre en évidence le milieu hypothétique servant de support aux ondes lumineuses dans l’espace, milieu auquel on avait donné le nom d’éther. Comme pour l’air, immobile et déformé par les ondes sonores, l’éther devait être immobile par rapport à la progression des ondes lumineuses, ce qui devait permettre de calculer la vitesse absolue de la terre dans l’espace. Deux physiciens américains,Michelson et Morley, mirent au point un appareil nommé interféromètre, censé mettre en évidence le mouvement de la terre relativement à l’éther. Cet appareil permettait de comparer la durée de trajet aller-retour d’une onde lumineuse émise vers un miroir dans le sens du mouvement de la planète, avec celui d’une onde lumineuse émise simultanément à 90 degrés vers un autre miroir. Emis dans l’éther fixe vers un miroir fuyant devant, le signal émis en avant devait être de retour après celui émis latéralement. Les expérimentateurs eurent beau tourner leur interféromètre dans tous les sens, ils n’observèrent aucun décalage dans la réception des signaux !
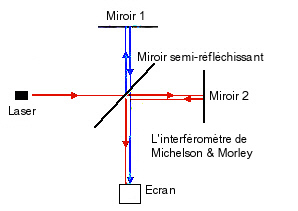
La conclusion logique était d’abandonner l’idée de l’éther, mais comment expliquer alors le comportement ondulatoire de la lumière ? Hendrik Antoon Lorentz supposa alors que la résistance de l’éther avait pour effet de contracter le bras supportant le miroir de l’interféromètre dans le sens du mouvement, de telle façon que cela compense exactement la différence attendue. La formule mathématique permettant de calculer la contraction du bras en fonction de la vitesse reçut le nom de transformation de Lorentz-Fitzgerald, le résultat étant exprimé par γ (gamma).
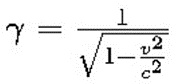
Einstein et la synchronisation des horloges
Les préoccupations d’Albert Einstein étaient toutes autres. Employé au Bureau des brevets à Berne, il s’est intéressé au problème de la synchronisation des horloges : comment faire en sorte que deux horloges, situées en des endroits très éloignés, soient parfaitement synchronisées. Le meilleur moyen pour les faire communiquer entre elles est d’utiliser un signal électromagnétique, en tenant compte de la vitesse de propagation du signal qui est celle de la lumière. L’exemple favori d’Einstein est celui d’un train en marche longeant le quai d’une gare. Pour synchroniser ses horloges, un observateur placé au milieu du quai ou du train va d’abord s’assurer de sa position en envoyant simultanément un signal vers chacune des extrémités de son référentiel et vérifier qu’il les reçoit bien simultanément en retour. Pour connaître la distance le séparant des horloges à synchroniser, chaque observateur va relever le temps mis par chaque signal pour faire l’aller-retour dans son référentiel et diviser le résultat par deux. Il ne lui restera plus qu’à envoyer un message réglant chaque horloge des extrémités sur l’heure de l’horloge centrale en tenant compte du temps nécessaire pour effectuer le trajet.
La synchronisation des horloges
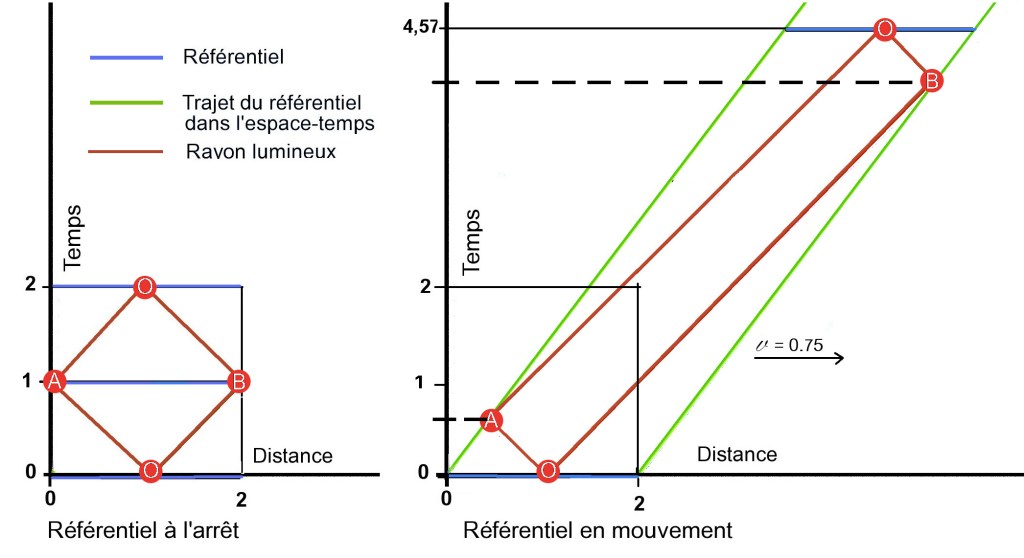
A gauche, le référentiel est à l’arrêt par rapport à un observateur immobile : les deux signaux (en rouge) sont émis simultanément et parcourent la même distance à l’aller comme au retour. Ils sont reçus simultanément par l’observateur O au centre du dispositif.
A droite, le référentiel est en mouvement : à son bord le signal envoyé vers l’avant prend d’abord du retard qu’il rattrape ensuite, alors que c’est l’inverse pour le signal envoyé vers l’arrière. L’observateur placé au centre du dispositif reçoit les signaux simultanément. Cependant, le trajet étant plus long, sa durée sera plus longue, ce qui mettrait le mouvement en évidence si les effets relativistes n’y remédiaient.
Selon la mécanique classique, à bord d’un mobile en mouvement inertiel, tout se passe comme si celui-ci était immobile, car tout ce qui s’y trouve est uniformément accéléré, d’où le premier postulat :
Toutes les lois de la mécanique sont les mêmes dans tous les référentiels d’inertie
Il devrait résulter, de la loi d’addition des vitesses de Newton, qu’à bord d’un mobile propulsé à la vitesse de la lumière, la vitesse propre des corps s’y mouvant dépasse celle de la lumière aux yeux d’un observateur extérieur immobile (addition illimitée des vitesses.)
En électromagnétisme, la vitesse de la lumière est invariable, d’où le second postulat :
La vitesse de la lumière est la même dans tous les référentiels d’inertie.
On en conclut que c’est une limite indépassable : aucun corps matériel ne peut aller plus vite.
Ces deux postulats sont incompatibles parce que le premier s’explique par la loi d’addition des vitesses que n’admet pas le second. L’impossibilité de dépasser la vitesse de la lumière est incompatible avec l’addition illimitée des vitesses telle que la concevait Newton. Contrairement à ce que pensait celui-ci, les vitesses ne s’additionnent pas à l’infini.
La résolution de la contradiction entre mécanique et électromagnétisme
La vitesse résulte du temps mis par un corps en mouvement pour parcourir une certaine distance. Dans la vie de tous les jours, elle est exprimée en kilomètres/heure, autrement dit en nombre de kilomètres parcourus en une heure : v (vitesse) = d (distance) / t (temps).

Si d’ > d et v’ = v, alors t’ > t, et t’ = d’ / v.
Mathématiquement cela se tient, mais comment la durée observée dans le train en mouvement par l’observateur immobile sur la voie peut-elle être plus grande que celle vécue à l’intérieur du train ? En réalité, la théorie de la relativité élaborée par Einstein affecte également les longueurs, dans les mêmes proportions. Lorsqu’un corps est en mouvement, le temps y est ralenti et les longueurs contractées. Cette idée semble incongrue car le temps et l’espace nous paraissent extérieurs aux choses, une sorte de scène où la matière se meut. La réponse d’Einstein est que rien n’impose la croyance en l’invariabilité des durées et des longueurs. Il faut abandonner cette idée préconçue et arbitraire, car c’est la seule façon de sortir de la contradiction. Et ça marche !
